Slide 0

I hope you're having a wonderful day. Welcome to this new episode, in which we’ll clarify what the mathematical term of probability is all about. We’ll start from the previous, rather intuitive concept and see that much of this is also found in the perspective of scientific mathematics.

Slide 1

Let’s start right here. We have – as stated – previously used a rather intuitive term. The starting point was always experiments with a discrete, finite set of outcomes.

Then we often counted and essentially stuck with the generally possible events and outcomes of real, simulated, or – also one time – presented counting when we interpreted the probabilities.

Here you see the typical examples from past episodes. We conducted Laplace experiments such as rolling a die or flipping a coin. And we also looked at non-Laplace experiments such as tossing a thumbtack.

Slide 2

Now we will try to express the term “probability” in a mathematically useful way, which means nothing more than we will strive for an exact definition. But of course, we won’t forget anything that we have worked out up to now.

Slide 3

Laplace probability is useful as a first approach to the mathematical term.

If you roll a normal die, then you of course assume that each of the numbers 1, 2, 3, 4, 5, and 6 have the same chance to be on top. This chance is 1/6 – we would feel that anything else is hardly plausible.

If you flip a coin, then accordingly heads or tails has the same chance of coming up. This chance is 1/2 and this is also the only plausible assumption.

Let’s put together a mathematical definition from these observations and assumptions.

Slide 4

We look at a random experiment with a finite set of outcomes and assume that all outcomes have the same chance of occurring, which means nothing more than they occur equally.

Then the probability for event E is defined as P(E) = the number of favorable cases divided by the number of possible cases. In other words: We divide the cardinality – which is the number of elements – of set E by the cardinality of set Ω.

Let’s look at examples; then the abstract math will become completely innocuous and understandable very quickly.

Slide 5

We roll a normal die and determine the Laplace probability for the event E = rolling a 5. Then P(E) is very clearly = 1/6.

There are six possible outcomes – namely, the numbers from 1 to 6 – and only one of them is “favorable”, thus the desired outcome, which is a 5.

Slide 6

We again roll a completely normal die and determine the probability for the event E = rolling a 5 or a 6. In this case:

P(E)=1/6 + 1/6 = 2/6 = 1/3.

There are six possible outcomes – all numbers from 1 to 6 – and only two of them are desired, a 5 and a 6.

Slide 7

Let’s roll the die again. We roll a normal die and determine the probability for the event E = either we roll a 5 or a 6 or a prime number.

Then there are four favorable outcomes, namely 2, 3, 5, and 6. We have E = {2, 3, 5, 6} and thus |E| = 4. This means P(E) = 1/6 + 1/6 + 1/6 + 1/6 = 4/6 and that is reduced to 2/3.

Slide 8

We repeat the experiment, roll a normal die, and again determine the probability for the event E = either we roll a 5 or a 6 or a prime number. But let’s give a reason for the outcome in a different way.

There are – very clearly – six possible outcomes, all numbers from 1 to 6. Two of them are “favorable” due to the first condition, namely a 5 and a 6, three are “favorable” due to the second condition, and those are the prime numbers 2, 3, and 5. However, now one number has been counted twice, the 5.

Thus we end up with P(E) = 2/6 + 3/6 − 1/6 = 4/6 = 2/3.

With these simple considerations, we have already created a framework for dealing with mathematical probability and here initially with Laplace probability. Let’s look at this more formally on the next slide.

Don't worry; it will all remain very simple.

Slide 9

First, we will look at an event E very generally and thus at the favorable outcomes from the set of all possible outcomes. Naturally, the number of favorable outcomes can always be at most the number of possible outcomes. If you describe this as a fraction, then the numerator is at most as great as the denominator and thus the value of the fraction is maximum 1.

Formally, we write this as: 0 ≤ P(E) ≤ 1 for all events E.

What if there are no favorable outcomes? Of course, then the numerator is a zero and the value of the fraction is zero.

Once again: If we define no possible event E as desired, thus favorable, then P(E) is clearly equal to zero. And if we view every outcome as favorable, then of course E must be the entire set Ω.

And we can also write this formally: P({ }) = 0 and P(Ω) = 1.

Finally, we look at independent events E₁ and E₂, each being outcomes that are viewed as favorable but which have no common elements. Clearly, we must then add the individual probabilities to arrive at the probability of E₁ and E₂ together.

Written formally:

P(E₁∪E₂) = P(E₁) + P(E₂) if E₁∩E₂ = { }

You thus see that this characteristic of Laplace probabilities is derived without straying from common sense.

In mathematics, we then look for a formal way of expression. No, certainly not to distance ourselves from the rest of the world. Rather, it’s about a clear representation that leaves no doubt of what it states. You know that our normal language cannot meet this requirement.

Slide 10

Now, not every random experiment is a Laplace experiment, and you see an example here.

We spin the wheel shown here. Ω = {1, 2, 3} and it also makes sense to assume: P(1) = ¼ , P(2) = ¼, P(3) = ½

In this case as well, any other determination wouldn’t seem plausible.

We would calculate the probability of landing on a 1 or a 2 in the same way, as P(1) + P(2) = ¼ + ¼ = ½.

You can have only 1 or 2 or 3 as an outcome, thus P(Ω) = 1. The pointer has to land somewhere.

A 4 doesn’t appear; the probability for this is zero. And that likewise applies to a 5, a 6, or a 7, or any other number that doesn’t appear on the wheel. These are impossible events.

We’ll formalize this on the next slide.

Slide 11

Here as well, 0 ≤ P(E) ≤ 1 for all events E, that is, the probability of each event E lies between 0 and 1.

P({ }) = 0 and P(Ω) = 1 also applies. An impossible event has a probability of 0; a certain event has a probability of 1.

Finally, P(E₁∪E₂) = P(E₁) + P(E₂) if E₁∩E₂ = { }. Remember: If the wheel comes to a stop at 1 or 2, we add the individual probabilities for 1 and 2 for this combined event.

Slide 12

We know that there are not theoretical assumptions about the outcome of every random experiment. We looked at the example of a thumbtack and tossed it 1,000 times. It landed on its head 633 times and on its side 367 times.

It therefore makes sense to assume that

P(head) = and P(side) = .

Of course, here the assumption can easily change in the next experiment or with a new kind of thumbtack.

Can we get on this nevertheless? Let’s try it.

Slide 13

Basic terms here are absolute and relative frequency.

If a random experiment is repeated multiple times, each event occurs at a specific frequency. This number is called absolute frequency.

For example, if a thumbtack is tossed 1,000 times and lands 633 times on its head, then 633 is the absolute frequency of the “head” event.

Generally speaking: If event A occurs k times in n experiments, then h_n(A) = k/n is the relative frequency of event A in this series of experiments.

If a thumbtack is tossed 1,000 times and lands 633 times on its head, then

h₁₀₀₀(head) := 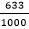= 0,633 = 63,3%.

This is the relative frequency of the “head” event.

Slide 14

The relative frequency is the starting point for defining the term probability, referred to as statistical probability.

The basic idea goes back to Richard von Mises, who lived from 1883 to 1953 and published it for the first time in 1919. We determine the relative frequency for a random experiment conducted a very high number of times, what we call the frequentist approach. In the process, we imagine that we could conduct the experiment an “infinite” number of times.

The statistical probability of an event A is defined as the limit of the relative frequency if one were to conduct the experiment an “infinite” number of times:

Sounds good, right? It also looks marvelous mathematically, right? Nevertheless, there are pitfalls that we will go into later. But first let’s take a look at the now familiar characteristics. I promise you, it will also work this time.

Slide 15

First, the tossed thumbtack lands on its side or its head. We can again assign a probability to the possible events, even if they were obtained experimentally. In any case, the number is between 0 and 1, whereby 0 characterizes the impossible event and 1 the event “either head or side”.

We have already written down the first two characteristics nice and formally: 0 ≤ P(E) ≤ 1 for all events E, P({ }) = 0 and P(Ω) = 1.

The third characteristic is also self-explanatory. Again, P(E₁∪E₂) = P(E₁) + P(E₂) if E₁∩E₂ = { }.

Slide 16

I already suggested that the term statistical probability is not without its problems. One major problem is that we cannot conduct a random experiment an infinite number of times. And for the finite case – which we have already seen – everything is subject to chance.

An example: On August 18, 1913, it is said that during a game of roulette at the Monte Carlo casino, the ball fell in a black field 26 times in a row. Many people lost a lot of money that day because they bet on another color too soon.

As a consequence, the concept of a limit as used in statistical probability cannot have the precision of the concept of a limit as known in calculus. This sort of thing is disliked in mathematics and that was a key reason for further research.

Slide 17

The breakthrough was achieved by Andrey Nikolaevich Kolmogorov, who published a book in 1933 in which he proposed an axiomatic concept of probability. Here are the axioms – which you all are already actually familiar with in the meanwhile. But let’s take things one at a time.

Let's assume that set Ω is a finite sample space. It’s fine for you to think of the six numbers of a die or the two possibilities of how the thumbtack lands. Now let’s assume that P is a mapping that assigns a real number to each event. P should thus assign a real number to all subsets of Ω The set of all subsets of a set is its power set and thus P is a mapping from the power set P(Ω) to the set ℝ.

This mapping P has a specific name. We call it probability distribution precisely when the following axioms are metS:

1. P(A) ≥ 0 for all A ∈ P(Ω).
2. P(Ω) = 1.
3. For events A, B ∈ P(Ω) with A ∩ B = {}, the following applies:
   P(A ∪ B) = P(A) + P(B).

Well, we had already worked out these axioms. For rolling dice as well as for spinning the wheel or tossing the thumbtack, thus for Laplace experiments and other random experiments.

Slide 18

We can describe these axioms aptly. The first axiom P(A) ≥ 0 for all A ∈ P(Ω) signifies non-negativity, because P has values that are greater or equal to zero.

The second axiom provides normalization. Because Ω contains all outcomes, the determination P(Ω) = 1 makes sense since then all events should reasonably assume a value between 0 and 1 under P.

And so that this works for sure, additivity follows as the third axiom. For events A, B ∈ P(Ω) with A ∩ B = { }, the following applies: P(A ∪ B) = P(A) + P(B).

Are these axioms indeed suitable? That’s not our concern here and now. At this point, we rely on the many examples that make this plausible.

Slide 19

And no, the axiomatic concept of probability will tell us nothing about how the matter with the thumbtacks will end in the long term.

However, it makes the matter mathematically crisis-proof and is the basis for calculations.

Here is an example. From the three axioms, we can derive that P({ }) = 0.

First, Ω ∩ { } = { }. This is very easily derived from the rules of working with sets.

We also know that P(Ω) = 1, the second axiom states this.

Now, P(Ω ∪ { }) = P(Ω) + P({ }) due to axiom 3 and we put it all together:

Thus, 1 = P(Ω) = P(Ω ∪ { }) = P(Ω) + P({ }) and so P({ }) = 0.

Slide 20

Was that too fast for you? No worries. I have listed the proof here again step by stept.

I have adopted the form – statements on the left and reasons on the right – from the Anglo-Saxon world. There, people speak of “two-column proofs.” Take a break and look at this in detail. You simply can’t understand mathematics only through listening.

Slide 21

And if you would like to practice a little more, then you could perhaps perform this proof:

Look at event A and its complementary event “not A”. Prove that P(A) + P(not A) = 1.

I definitely recommend that you write this proof in two columns.

Slide 22

Here is the solution. Take all the time you need to look at it.

Slide 23

That’s all for today. Many thanks for being here. I look forward to seeing you in the next episode.