Slide 0

Welcome to this new episode. Today we want to remind you a little bit about school lessons that are related to statistics in a broader sense. We’re talking about the binomial theorem and Pascal’s triangle.

Slide 1

Let’s begin with the binomial theorem. We’ve already talked about this because this theorem is a useful tool for looking at situations in statistics and probability.

What do we want today? To understand it exactly and then also to prove it. Is that okay with you? Are you ready for the new episode? Then let’s talk about mathematics.

Slide 2

Certainly, you remember the binomial theorem in its simplest form. (a+b)² = a² +2ab + b² for all real numbers a and b. You can very easily calculate this according to the rules for the product of two elements.

(a+b)² = (a+b) • (a+b) = a² + ab + ba + b² and because the commutative law applies to the multiplication of real numbers, a² + ab + ba + b² = a² +2ab + b² . This is easy, but admit it, it’s also pretty boring.

Slide 3

Methods that show the validity graphically are also useful for class. You see an example here. In a square with a side length of a+b, you can conveniently draw in a square with side length a and a square with side length b. At the same time, you end up with two rectangles with sides a and b. Of course, this isn’t a proof in the traditional sense, but it makes the theorem very plausible.

Slide 4

By the way, you can also represent the formulas for (a-b)² and (a+b)•(a-b) in a similar manner, but that would distract us from the topic. Try it out yourself.

Slide 5

Because drawing in three or even more dimensions is not an easy exercise and maybe impossible, it really isn’t useful for n > 2. However, multiplication also very quickly becomes cumbersome. Here you see the results for n=3, n=4, n=5 and n=6. Continuing in this way by hand wouldn’t be any fun. As is almost always the case, here as well we need a way to view this systematically.

Slide 6

But it’s very clear that the coefficients develop one from another with each new equation.

For (a+b)², the elements a² and b² each occur once. This applies accordingly to (a+b)³ and the elements a³ and b³, to (a+b)⁴ and the elements a⁴ and b⁴, to (a+b)⁵ and the elements a⁵and b⁵, to (a+b)⁶ and the elements a⁶ and b⁶.

You can easily see that further multiplication with a+b would make a⁷ and b⁷ and generally that in (a+b)ⁿ, the elements aⁿ and bⁿ each occur once.

Let’s look again at the step from (a+b)² to (a+b)³. Through multiplication with a+b, the element 2ab becomes 2a²b and 2ab² one time each. The elements a²b and ab² result once each from a² and b².

We can further view this systematically. Please look at this yourself; a verbal explanation could be difficult to follow here.

Slide 7

However, you can easily determine (a+b)⁷ from the row above it.

It is (a+b)⁷ = a⁷ + 7a⁶b + 21a⁵b² + 35a⁴b³ + 35a³b⁴ + 21a²b⁵ + 7ab⁶ + b⁷.

Slide 8

The coefficients form a Pascal’s triangle. Each coefficient is the sum of the two coefficients above it. A “1” is always at the “edges”.

Slide 9

You can also write this Pascal’s triangle like this, namely using the binomial coefficients. What exactly is going on here?

Slide 10

We determine the following. The element “n choose k” is called a binomial coefficient. The name makes sense because it is clearly determined by the coefficients in the Pascal’s triangle. It is read (and we already used this) as “n choose k”. In this element, n is a natural number, k is a natural number or 0, and k ≤ n.

But remember: We already defined this term in another place. Can you do that twice? Of course not. Rather, we must show that the two concepts are identical.

Slide 11

We saw this in episode 7 (remember that Nina wanted to pack exactly 5 of her 12 dresses in her suitcase):

The set of numbers k subsets of a set with n elements is n! / k! • (n-k)!. At that time, we called this number also “n choose k” – of course, using the same notation.

Slide 12

We make the identity of the two plausible using the proven method step by step. In the first step, we look at (a+b)⁰ = 1.

We’ll proceed here as usual and accordingly won’t hassle with . We set : = 1.

Slide 13

In the second step, we look at and . We can calculate this according to the rule and come up with

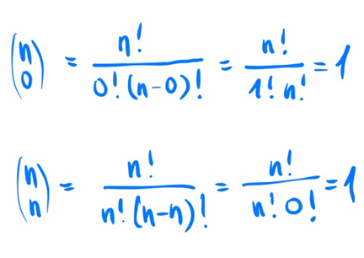
Slide 14

In the third step, we show that = n =  for all natural numbers n. It thus also fits accordingly with the second and second-to-last number in a row of the triangle.

The steps are quite similar to what we did before. We just use the formula and come out with = n = .

Slide 15

The fourth step explains the symmetry of binomial coefficients. We show that for all natural numbers n, with k < n or k=0.

Slide 16

The fifth step requires the most calculating.

We show here that for all natural numbers n. It thus fits that two adjacent numbers in Pascal’s triangle result in the number below them when added together. We thus calculate and .

Once more, this is not difficult. It’s just a matter of reading carefully and using the formula.

Slide 17

We calculate the sum of these two elements. First, we need to determine the common denominator of the two fractions. That is clearly (k+1)! • (n-k)!.

Slide 18

Then it looks like this.

And so we have a nice calculation of and .

Slide 19

And this is how we come to the solution:

The sum of and is the sum of the two elements we just had on the previous slide and this may be calculated to .

Slide 20

In general, you arrive in this way at the binomial theorem.

For all real numbers a and b and all natural numbers n, the following applies:

Slide 21

So much for the statement and also for an algebraic approach to the problem.

Here as well, people may not intuitively understand some things and there are misinterpretations. In a study by Fischbein and Schnarch in 1997, the participants had difficulties with this task:

If a committee wants to select two members from ten candidates, there are

• more
• fewer or
• the same number of

possibilities than for selecting eight members from ten candidates. In grade 11, 15% of the students gave a correct answer, and in a group of teacher students only 6%. Most people thought that there are more possibilities for selecting two persons from ten than for eight persons from ten.

We have just gone to a great deal of trouble to show that there is no difference, because 10 choose 2 is the same as 10 choose 8. But apparently this is not very intuitive.

Slide 22

That’s all for today. Many thanks for being here. See you the next time.