Computational Thinking im
MINT-Unterricht

Computational Thinking: Kompetenzen für
die digitale Welt

Ziel von Computational Thinking im MINT-Unterricht ist es, die Kompetenz von Schülerinnen und Schülern zu stärken sowie Aspekte realweltlicher Probleme zu identifizieren, die für eine informatische Modellierung geeignet sind. Sie lernen, algorithmische Lösungen für (Teil-)Probleme zu bewerten und selbst zu entwickeln. Damit vermittelt die Methode Kompetenzen, die auch von der Kultusministerkonferenz (KMK, 2016) im Kompetenzbereich „Problemlösen und Handeln“ gefordert werden: Schülerinnen und Schüler sollen Algorithmen erkennen und formulieren können. Diese Ausbildung von Kompetenzen für die digitale Welt gehört zur Aufgabe aller Schulfächer. Durch die Einbindung der Informatik in die MINT-Fächer sind hier besondere Anwendungsmöglichkeiten gegeben, komplexe Problemstellungen zur Bearbeitung von Lösungsansätzen strukturiert zu fassen.

Methode     Medien     Forschungsartikel     Quellen

Jeanette Wing, Pionierin auf dem Gebiet von Computational Thinking, sieht darin eine grundlegende Fähigkeit, die alle erlangen sollten, nicht nur Informatiker/-innen. Zum Lesen, Schreiben und Rechnen sollte den analytischen Fähigkeiten jedes Kindes Computational Thinking hinzugefügt werden.

Einsatz in der Schule

Bei Computational Thinking geht es darum, ein komplexes Problem zu verstehen, dieses auf die wesentlichen Teile zu abstrahieren und in kleinere Teilprobleme zu zerlegen. Auch die Beschreibung einer algorithmischen Lösung des Problems sowie die Prüfung und Übertragung der Lösung auf andere Kontexte sind Teile von Computational Thinking.

Obwohl Computational Thinking sich aus der Informatik entwickelt hat, entfalten die Methoden und Prinzipien des Ansatzes auch in anderen Bereichen eine effektive Wirkung. Insbesondere in verwandten Schulfächern der Informatik, etwa in Naturwissenschaft und Technik, können viele Verbindungen hergestellt werden. Computational Thinking bedeutet dabei keineswegs, so zu denken wie ein Computer, sondern bezeichnet vielmehr Problemlösungsfähigkeiten, die sich auf viele verschiedene Fragestellungen im MINT-Unterricht anwenden lassen. Es handelt sich um ein fächerübergreifendes Konzept. Tätigkeiten wie das Programmieren können eine Rolle spielen, müssen es aber nicht.

Der methodische Hintergrund

Der Begriff Computational Thinking wurde bereits im Jahr 1980 zur Förderung von mathematischen Problemlösungskompetenzen bei Schülerinnen und Schülern eingeführt (Papert, 1980). Er wurde von Jeanette Wing (2006) wieder aufgegriffen, um zu unterstreichen, dass Computational Thinking eine grundlegende Fähigkeit nicht nur für Informatikerinnen und Informatiker ist, sondern zu den Grundfertigkeiten jeder Person zählen sollte.

Die zentralen methodischen Komponenten sind dabei:

• Abstraktion zur Reduktion von Komplexität, um die wesentlichen Bestandteile der Problemstellung zu verdeutlichen
• Zerteilung, um ein Problem in mehrere kleinere lösbare Teilprobleme zu unterteilen
• Design, also die Entwicklung der Lösung aus der abstrahierten, zerteilten Problemstellung
• Analyse der Lösung

Diese methodischen Komponenten werden durch bestimmte Haltungen ergänzt, die den Problemlösungsprozess fördern. Problemlösen ist ein Prozess, der eine systematische Beobachtung und kritisches Denken beinhaltet, damit Lernende sich ganzheitlich in Lernprozessen orientieren können. Die Methoden und Prinzipien von Computational Thinking unterstützen dabei das Verstehen und Interpretieren der Bedeutung von Informationen auf dem Weg der Lösungsfindung.

Im Fokus:
Algorithmen

Der Begriff Computational Thinking entwickelte sich über einen längeren Zeitraum und wurde zunächst von dem Mathematiker Seymour Papert 1980 vor dem Hintergrund des Problemlösens in der Mathematik in der Computerprogrammierung eingeführt. Die aktuelle Bewegung zu Computational Thinking wurde eingeleitet, als Wing den Begriff 2006 wiedereinführte und den Schwerpunkt auf das Lösen von Problemen entlang informatischer Herangehensweisen legte, ohne unbedingt einen Computer in den Prozess einzubeziehen (Dagiene and Sentance, 2016). Computational Thinking umfasst dabei insbesondere die Suche nach algorithmischen Beschreibungen eines Lösungswegs. Auch wenn ein Computer nicht zum Einsatz kommen muss, sind algorithmische Denkweisen somit Teil von Computational Thinking. So vereint der Ansatz verschiedene Methoden, Techniken und Systematiken, die in der Informatik zur Lösung von Problemen verwendet werden können.

Teilschritte von Computational Thinking

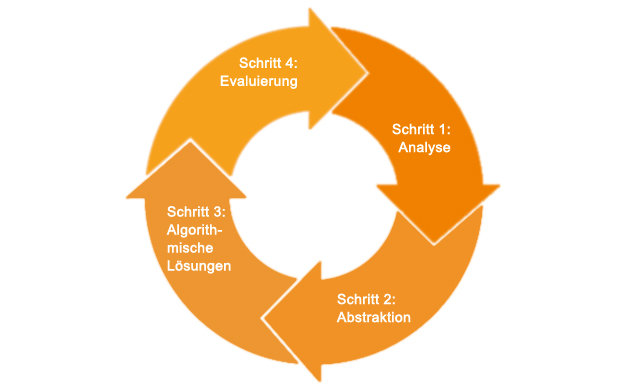
Der Problemlösungsprozess mit Computational Thinking im MINT-Unterricht soll dazu befähigen, komplexe Probleme nicht nur zu lösen, sondern die Lösungswege auch auf andere Probleme anwenden und somit Komplexität für sich systematisch abbauen zu können. Daher wird folgender schrittweiser Prozess zur Lösung eines Problems vorgeschlagen:

Wenn eine Problemstellung Ähnlichkeiten mit einem anderen Problem aufweist, von dem die Lösung schon bekannt ist, können daraus Lösungsstrategien abgeleitet werden.

Förderung von Haltung durch Computational Thinking

Computational Thinking umfasst nicht nur einen linearen Problemlösungsprozess mit den wichtigen informatischen Konzepten „Zerlegung und Abstraktion“, sondern es fördert zugleich bestimmte Haltungen bzw. Einstellungen zur Bewältigung von Problemen:

• Durchhaltevermögen bei der Arbeit mit schwierigen Problemen
• Mehrdeutigkeiten akzeptieren können
• Sicherheit im Umgang mit Komplexität
• Kompetenz, mit offenen Lösungswegen umzugehen
• Fähigkeit zur Kommunikation und zur Zusammenarbeit mit anderen, um ein gemeinsames Ziel oder eine Lösung zu erreichen

Über den Autor

Jun.-Prof. Dr. Bernhard Standl
Tenure-Track-Professor für Informatik und ihre Didaktik an der Pädagogischen Hochschule Karlsruhe. Seine Forschungs­schwerpunkte liegen im Bereich der Modellierung von Lehrkonzepten als didaktische Entwurfsmuster im Kontext von Computational Thinking.

Medien für den Einsatz der Methode

Computational Thinking forschend erlernen: Online Fortbildungsmodul für MINT-Lehrkräfte
Viele Lehrkräfte fördern bereits Teil-Aspekte von Computational Thinking, ohne sich dessen bewusst zu sein. In dem Online-Modul zu Computational Thinking werden die Problemlösungsvorgänge erklärt und neue Ideen für ihre Integration in den MINT-Unterricht gegeben. Denn Problemlösungskompetenz spielt im naturwissenschaftlichen Unterricht, insbesondere im Kompetenzbereich der Erkenntnisgewinnung, eine zentrale Rolle. Durch Forschendes Lernen kann an die naturwissenschaftliche Erkenntnisgewinnung herangeführt werden. Daher wird Computational Thinking in der Online-Anwendung zur Fortbildung Experimento | 10+ vertieft und mit dem Forschenden Lernen verknüpft.

Quellen

Barr, V. & Stephenson, C. (2011): Bringing Computational Thinking to K-12. In: ACM Inroads 2(1), S. 48.

Dagiene, V. & Sentance, S. (2016): It’s Computational Thinking! Bebras Tasks in the Curriculum. In: Informatics in Schools: Improvement of Informatics Knowledge and Perception. ISSEP 2016. Lecture Notes in Computer Science 9973, S. 28–39.

Dede, C. (2010): Comparing frameworks for 21st century skills. In: 21st century skills: Rethinking how students learn 20(2010), 51-76.

Kultusministerkonferenz KMK (2016): Bildung in der digitalen Welt: Strategie der Kultusministerkonferenz. S. 18. Verfügbar unter: https://www.kmk.org/fileadmin/Dateien/veroeffentlichungen_beschluesse/2016/2016_12_08-Bildung-in-der-digitalen-Welt.pdf

Lee, I. et al. (2011):Computational Thinking for Youth in Practice. In: ACM Inroads 2(1), S. 32.

Papert, S. (1980): Mindstorms: Children, Computers, and Powerful Ideas. New York: Basic Books.

Polya, G. (1957): How to Solve It. 2. Ausgabe, London: Penguin Books Ltd.

Wing, J. (2006): Computational Thinking. In: Communications of the ACM 49(3), S. 33.