24 The goat problem

Slide 0

Welcome to this new episode. We’re going to talk about mathematics again. This episode is about a goat and a problem that it can cause. Well, and also about conditional probability.

Slide 1

Multistage random experiments and conditional probabilities – we’ve already addressed these topics in the previous episode. It did not get all that complicated because we limited ourselves to two-stage random experiments. But of course, it can also be more complex. Have no fear, it will get just a little bit more complicated.

Slide 2

We’ll begin with a very simple case that is also very practical to conduct. We will flip a coin three times and observe the probability with which it comes up “tails” exactly two times.

This is quite clear mathematically.

P(tails) = P(heads) = 1/2.  Accordingly, the probability of a particular order of heads and tails is thus 1/2 • 1/2 • 1/2 = ½³ = 1/8.

Altogether, there are eight possibilities.  We consider how many of them are “favorable.”

Slide 3

A tree diagram is useful here because we can plot any number of stages, at least theoretically. And we easily see the result. Of the eight possible cases, there are three in which tails comes up twice. They are marked with a green dot here.

Slide 4

Now, sometimes we must take conditions into account, and we will look at an example of this.

Mara is a neighbor of Aida and Nio. Her cat has had four kittens.

Nio knows that one of the kittens is male.  Aida says that she even saw two male kittens. Are any of the kittens female? The two think about this – initially independently of each other.

Slide 5

Nio ponders that of the five theoretical possibilities, – there are zero, one, two, three, or four female kittens – there is only one possibility that none of the kittens are female. So four possibilities remain

in this case 

(0 f, 4 m; 1 f, 3 m; 2 f, 2 m; 3 f, 1 m; 4 f, 0 m) of the distribution, one is that there are only female kittens. Due to Nio’s information, this possibility can be ruled out. Four possibilities remain, of which three are favorable: He therefore gives a probability of 3/4 for at least one female kitten.

Aida has more information, so she can rule out two of the five possibilities right away. Of the three remaining possibilities, two are favorable: She arrives at the lower probability of 2/3 for a female kitten in the litter.

Slide 6

Yes, apparently the assessment of the probability of an event is not necessarily fixed. Rather, it can depend on different information. And that’s exactly what the goat problem is about.

Slide 7

Imagine that you are on television. On a game show, the grand prize is a brand new and beautiful car and only a single question separates you from it. However, you need a little bit of luck to answer this question. Well, mathematical knowledge can’t really hurt either.

Slide 8

Here is the situation.

You’re standing in front of three doors – closed, of course. Behind one door is hidden a beautiful, brand-new car that you would really like to have. Behind the other two doors there are goats. You may select one door and trust your luck.

Let’s assume you choose door 1. Now the moderator – who knows the answer to the problem – opens a door; not the door you chose, but door 3. A goat is standing behind door 3. The moderator asks you whether you want to keep your original selection or whether you would rather have him open door 2.

What do you think? Isn’t it all the same which of the two doors you select? Or is there a higher chance of winning with one of the two doors?

Take a guess.

Slide 9

We’ll take a close look at the situation, as we so often do. In the first step, you select any door. The probability that the car is behind that door, that is, the chance of winning, is very clearly 1/3. Exactly one of the three possible cases is favorable.

Slide 10

The moderator comes along in the second step. He opens door 3. The excitement builds. What is behind the door?

Slide 11

And we see a goat behind the door. Where then is the car?

Let’s assume you had selected door 1 and now you’re considering whether switching is favorable. There are (clearly) still these three possibilities:

The grand prize is behind door 1 or the grand prize is behind door 2 or the grand prize is behind door 3.

Slide 12

Let’s go through the situations.

Let’s assume that the grand prize is behind door 1. Then you will have simply had bad luck if you switch.

However, let’s assume that the grand prize is behind door 2. Then the moderator cannot open door 1 because you suggested that and he cannot open door 2 because the grand prize is there. He opens door 3, and switching to door 2 is favorable for you.

Let’s assume that the grand prize is behind door 3. Then the moderator cannot open door 1 because you suggested that and he cannot open door 3 because the grand prize is there. He opens door 2, and switching to door 3 is favorable for you.

In other words: In two of the three situations, switching is favorable for you and your probability of winning increases to 2/3.

Slide 13

And now very systematically. These are the events:

G_i := the grand prize is behind door i (for i = 1,2,3).

M_i := the moderator opens door i (for i = 1,2,3).

At the beginning, everything is actually quite simple for you and does not require any serious thinking. You do not have any information and therefore P(G₁) = P(G₂) = P(G₃) = 1/3.

Slide 14

Now, you have chosen door 1 and we assume that the moderator has opened door 3.

We are therefore looking for P(G₁|M₃) and P(G₂|M₃).

This requires a little work beforehand. We consider the probability that the moderator will open door 2 or door 3. And of course, we consider that you have selected door 1.

Slide 15

You have chosen door 1 and the moderator has opened door 3. We have just seen the possibilities in this case. Let’s scrutinize them again.

Why is P(M₃|G₁) = ½?

You say “door 1” and in this case that would be the grand prize. The moderator can freely choose to open door 2 or door 3. The probability that he will open door 3 is thus ½. 

Why is P(M₃|G₂) = 1?

You say “door 1” and a goat is standing behind this door. The moderator now cannot open door 1 (your selection) or door 2 (grand prize!!!). He will for certain select door 3.

Why is P(M₃|G₃) = 0?

Well, this would really go against the point of the game.

Slide 16

We take – and this is an important detail – the moderator’s viewpoint. Here is an overview; you’re already familiar with the numbers.

Slide 17

Do you recall Bayes’ theorem?

There is an expansion for it that allows us to solve the problem using a formula (and you can find the substantiation in relevant literature). We need

                           

                  P(M₃|G₂) = 1                     P(M₃|G₃) = 0

and calculate

 

 

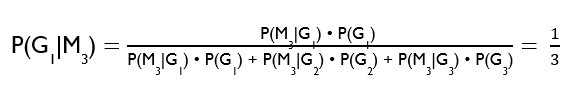
Once again, worded another way. The probability for door 1 was previously one third and does not change. Due to the additional information, the probability increases for door 2.

Slide 18

What have we done today?

Somehow, once again we have learned something about our poor intuition for stochastic correlations.  But that wasn’t all. We have seen that the particular point of view plays a role.

• With the goat problem, it is key for the assessment that the moderator knows the correct answer.
• With the kittens as well, it was the specific information that influenced the determination of the probabilities.

Conclusion: Conditional probability is not primarily about formulas and calculations, but first about reasonably interpreting a stochastic situation.

Slide 19

Thanks for listening; this wasn’t easy today. Maybe it will comfort you that some time ago intense discussions took place about the problem and its correct answer and that full-grown mathematicians were also wrong. Until next time. I look forward to seeing you.