25 The most difficult aspect of combinatorics: A totally unfair distribution of apples to children.

Slide 0

Welcome to a new episode. Today we will again talk about combinatorics and solve a problem that we have put off, and rightly so. We will hand out apples to children and leave all fairness out of the game.

Slide 1

Do you recall the urn models?

We already worked with them in the early episodes and drew balls from an urn. The important aspect was the difference in drawing the balls:

• with and without replacing the balls, and
• with and without taking the order into account

If we combine these possibilities, then there are four different ways of doing this. However, until now we have addressed only three cases.

Let’s take a brief look back to see what these three cases were and allow us to at least review the corresponding formulas.

Slide 2

This was the first case we looked at: Sampling with replacement while taking the order into account. And that was a relatively simple case.

Let’s look at the example. In this urn there are eight balls of different colors. Therefore, there are eight possibilities for drawing one of these balls. If you do this several times in succession and replace the ball each time, then you have these same eight possibilities each time you draw a new ball. Accordingly, if you draw a ball five times, you arrive at

8 • 8 • 8 • 8 • 8 = 8⁵ = 32,768

possibilities. This is sampling with replacement while taking the order into account.

Slide 3

In general, this is what it looks like: From a set with n elements, you can form

n • n • n • … • n = n^k

so-called k-tuples. We also called this words with a length of k.

Slide 4

Another case was about sampling without replacement while still taking the order into account.

You see the example. From an urn with eight different balls, you can initially select one of eight balls. In the next step, the drawn ball is missing, of course, and so you can select from only seven balls. If you draw five balls in succession, this results in 8 • 7 • 6 • 5 • 4 possibilities. And you can also write this as .

Slide 5

This is what it looks like in general:

From a set with n elements, you can draw  arrangements from k elements. You call these arrangements k-permutations.

Slide 6

And this was the third case we looked at. We draw again without replacement and we are not interested in the order.

You’re already familiar with this example: Amara likes to travel; she has five dresses. How many possibilities does she have to pack three of them in her suitcase?

Again, there are five possibilities for the first dress, four possibilities left for the second dress, and finally three possibilities for the third dress.

Slide 7

Is 5 • 4 • 3 therefore the solution? No, of course not. It doesn’t matter at all whether she takes the red dress first and then the green from the wardrobe or these two dresses in the other order. Therefore, it is necessary to count all identical combinations only once.

Slide 8

And that means dividing by 3! for three dresses. So, in this case there are

 

different possibilities.

Slide 9

In general, this is what it looks like. For sampling without replacement and without taking the order into account, we are interested in the number of subsets with k elements from a set with n elements. This number is .

Slide 10

Obviously, we’re still missing the case in which we draw one ball from an urn, replace it, but we’re not interested in the order.

Here is an example: We distribute eight apples to five children. How many different distributions are possible? In the process, we will very deliberately accept harsh unfairness. Accordingly, it can happen that one child does not receive an apple at all or that a child is given several apples.

Take a moment and think about why this example is fitting. Who or what is actually being drawn here?

Slide 11

No, naturally we are not going to put any children in an urn.

But how would it be if we use five balls that we label with the numbers from 1 to 5? Each number stands for a child. When a ball is drawn, the corresponding child is given an apple.

This is clearly sampling with replacement without taking the order into account.

The problem now is finding a suitable model for this situation in order to derive the number of possibilities (and a sensible formula).

Slide 12

Let’s use a table. Three possible distributions are entered as examples here. In the first case, child 3 goes empty-handed, and in the second case, child 5 has the bad luck and child 4 receives quite a lot. Finally, in the third case, child 5 goes home with all eight apples. As we said, we’re not at all interested in fairness.

And very clearly, there are many other possibilities for this distribution.

Slide 13

And now I ask you to view the situation a bit differently. Forget about the children, forget about the apples; view the table as something abstract.

Each table row can be understood as a sequence of 5 + 8 - 1 symbols. There are eight x’s and four bars. It is the bars that separate the individual cells of a row from each other. And of course there are five cells – just as the task specifies. Therefore, we do not write 4 bars, but choose the notation 5-1.

Slide 14

Once more, each row of the table can be understood as a sequence of 5 + 8 - 1 symbols, namely 8 x’s and 4 = 5 - 1 bars. We’re thus looking for possible positions for eight x’s.

But we just had precisely that.

For the distribution of the 8 x’s among the 5 + 8 -1 symbol positions when the order doesn’t matter and no repetitions are allowed, there are exactly

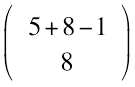 possibilities.

Slide 15

We can easily calculate this and come up with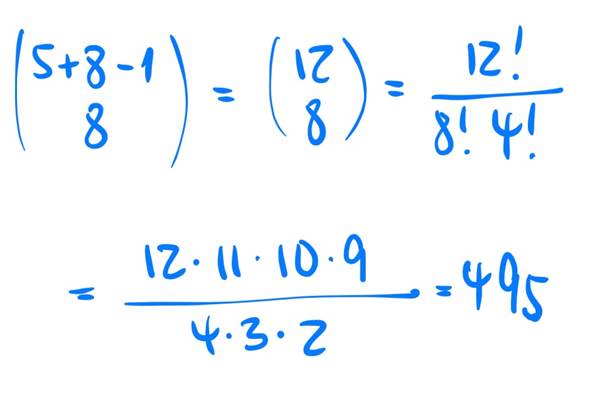

Slide 16

In general, this is what it looks like: If we select k objects from an urn with n objects with replacement and without taking the order into account, then there are

Slide 17

I don’t know how well you liked the model. Would you like a second way of explaining this? Here is another approach to solving the problem.

We again assume eight apples, A₁, A₂, … , A₈, and five children, K₁, … , K₅. We enter both “objects” as points on a graph.

Slide 18

You can plot the apples above the children who receive them. In the example here, the first and third children each receive two apples, the fourth child receives one apple, and the fifth child receives three apples. The second child goes empty-handed. If you consider the children and apples, that is, the X-axis and the Y-axis, then every possible allocation is a path on this graph.

Slide 19

Here is another path, but it is equally long. Actually, it’s quite simple. There are eight vertical connections that each stand for one apple and four horizontal connections, the spaces between the children on the X-axis.

Slide 20

Here is yet another possible path. And what does it look like if we proceed systematically?

Then we’re looking for all paths with a length of 12 consisting of eight vertical and four horizontal segments.

And obviously it is like this: You select the vertical segments, and the horizontal segments are fixed.

As a result, we’re back at the basic idea that we must select “8 from 12.”

Slide 21

When sampling objects with replacement and without taking the order into account, we must generally determine the number of k combinations with repetitions from a set with n elements, which is

 

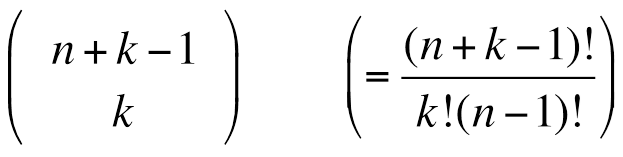
A k combination with repetition is another expression for a k-tuple or a word with a length of k.

Slide 22

Actually, for the paths with a length of 12, wouldn’t we have to be able to select the horizontal segments first? If so, then the vertical segments would be fixed.

Can that work? Wouldn’t that result in an entirely different number?

No, it works without a problem.  We already know:

Slide 23

Would you like to calculate an example yourself? Here it is.

Jo has six identical smiley stickers. He would like to stick them on 10 packets. How many possibilities (even if completely unfair) does he have for distributing his stickers on the packets? Take a short break, think about it, and calculate.

Slide 24

Sebastian has six identical smiley stickers, so n = 6. He would like to stick them on 10 packets, so k = 10.  And so you calculate as follows:

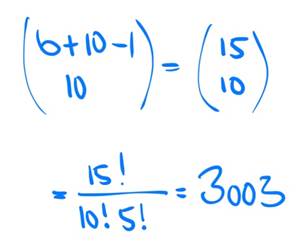
Slide 25

Let’s summarize.

There are the four following possibilities for selecting k elements from a set with n elements. You can sample the objects with or without replacement, and you can take the order into account or not. We have worked out a formula for each of these four cases, and you see them here in the table.

But don’t forget that especially in class, it cannot be just about using a formula. You should really understand the formula beforehand.

Slide 26

Thanks for being here. I look forward to seeing you in the next episode when we talk about mathematics again.