Folie 0

Einen wunderbaren guten Tag und herzlich willkommen. Wir werden in dieser Folge klären, was es mit dem mathematischen Begriff der Wahrscheinlichkeit auf sich hat. Wir gehen von dem bisherigen, eher intuitiven Konzept aus und werden sehen, dass sich viel davon auch in der fachlichen Betrachtungsweise der Mathematik wiederfindet.

Folie 1

Lassen Sie uns genau hier anfangen. Wir haben – wie gesagt – bisher einen eher intuitiven Begriff genutzt. Der Ausgangspunkt waren immer Experimente mit einer diskreten und endlichen Ergebnismenge.

Dann haben wir ganz oft gezählt und uns bei der Interpretation von Wahrscheinlichkeiten wesentlich an die prinzipiell möglichen Ereignisse und Ergebnisse des realen, simulierten oder auch einmal vorgestellten Zählens gehalten.

Sie sehen hier die typischen Beispiele der vergangenen Folgen. Wir haben Laplace-Experimente durchgeführt wie den Wurf eines Würfels oder einer Münze. Und wir haben auch Nicht-Laplace-Experimente betrachtet wie den Wurf einer Reißzwecke.

Folie 2

Darum geht es nun: Wir versuchen, den Begriff der Wahrscheinlichkeit mathematisch brauchbar zu fassen und das heißt nichts anderes, als dass wir eine exakte Definition anstreben. Aber natürlich vergessen wir dabei nichts von dem, was wir uns bisher erarbeitet haben.

Folie 3

Ein erster Zugang zum mathematischen Begriff bietet sich über die Laplace-Wahrscheinlichkeit an.

Wenn man mit einem normalen Würfel wirft, dann geht man ja davon aus, dass jede der Zahlen 1, 2, 3, 4, 5 oder 6 die gleicht Chance hat, oben zu liegen. Diese Chance beträgt 1/6 – alles andere würden wir als wenig plausibel empfinden.

Wirft man eine Münze, dann wird entsprechend Kopf oder Zahl mit gleicher Chance oben liegen. Diese Chance beträgt ½ und auch das ist die einzig plausible Annahme.

Lassen Sie uns aus diesen Beobachtungen und Annahmen eine mathematische Definition zusammenstellen.

Folie 4

Wir betrachten ein Zufallsexperiment mit endlicher Ergebnismenge und nehmen an, dass alle Ergebnisse mit gleicher Chance auftreten und das heißt nichts anderes, als dass sie gleichberechtigt auftreten.

Dann ist die Wahrscheinlichkeit P(E) für das Ereignis E definiert durch P(E) = Anzahl der günstigen durch die Anzahl der möglichen Fälle. Anders ausgedrückt: Wir teilen die Mächtigkeit – und das ist die Anzahl der Elemente – der Menge E durch die Mächtigkeit der Menge Ω.

Lassen Sie uns Beispiele betrachten, dann wird die abstrakte Mathematik ganz schnell völlig harmlos und verständlich.

Folie 5

Wir werfen mit einem normalen Würfel und bestimmen die Laplace-Wahrscheinlichkeit für das Ereignis E = Würfeln einer „5“. Dann ist P(𝐸) ganz offensichtlich =1/6.

Es gibt sechs mögliche Ergebnisse – nämlich alle Zahlen von 1 bis 6 – und nur eines davon ist ein günstiges, also gewünschtes Ergebnis und das ist die 5.

Folie 6

Wir werfen noch einmal mit einem ganz normalen Würfel und bestimmen die Laplace-Wahrscheinlichkeit für das Ereignis E = Würfeln einer „5“ oder einer „6“. Dann ist

P(𝐸)=1/6 + 1/6 = 2/6 = 1/3.

Es gibt sechs mögliche Ergebnisse und das sind alle Zahlen von 1 bis 6, Und nur zwei davon sind gewünscht, also günstige Ergebnisse und das sind die 5 und die 6.

Folie 7

Lassen Sie uns noch einmal würfeln. Wir werfen mit einem normalen Würfel und bestimmen die Wahrscheinlichkeit für das Ereignis E = entweder würfeln wir eine „5“ oder eine „6“ oder eine Primzahl.

Dann gibt es vier günstige Ergebnisse, nämlich 2, 3, 5 und 6. Es ist E = {2, 3, 5, 6} und somit |E| = 4. Also ist P(E) = 1/6 + 1/6 + 1/6 + 1/6 = 4/6 und das ist gekürzt 2/3.

Folie 8

Wir wiederholen das Experiment, werfen mit einem normalen Würfel und bestimmen noch einmal die Wahrscheinlichkeit für das Ereignis E = entweder würfeln wir eine „5“ oder eine „6“ oder eine Primzahl. Aber lassen Sie uns das Ergebnis auf eine andere Art begründen.

Es gibt – ganz klar – sechs mögliche Ergebnisse und zwar alle Zahlen von 1 bis 6. Zwei davon sind „günstig“ wegen der ersten Bedingung, nämlich die 5 und die 6, drei sind „günstig“ wegen der zweiten Bedingung und das sind die Primzahlen 2, 3 und 5. Nun wurde aber eine Zahl doppelt gezählt und das ist die 5.

Also bekommt man P(𝐸) = 2/6 + 3/6 − 1/6 = 4/6 = 2/3.

Mit diesen einfachen Überlegungen haben wir bereits ein Gerüst für den Umgang mit der mathematischen Wahrscheinlichkeit und hier zunächst einmal mit der Laplace-Wahrscheinlichkeit geschaffen. Lassen Sie uns das auf der nächsten Seite formaler betrachten.

Keine Angst, es bleibt alles ganz einfach.

Folie 9

Zunächst betrachten wir ganz allgemein ein Ereignis E und damit die günstigen Ergebnisse aus der Menge aller möglichen Ergebnisse. Natürlich kann es immer nur höchstens so viel günstige wie mögliche Ergebnisse geben. Wenn man das als Bruch schreibt, dann ist der Zähler höchstens so groß wie der Nenner und damit ist der Wert des Bruches höchstens 1.

Formal schreibt man: Es ist 0 ≤ P(E) ≤ 1 für alle Ereignisse E.

Und wenn es gar keine günstigen Ergebnisse gibt? Naja, dann steht im Zähler die Null und der Wert des Bruches ist Null.

Noch einmal: Wenn wir gar kein mögliches Ereignis E als gewünscht, also günstig festlegen, dann ist P(E) offensichtlich gleich Null. Und wenn wir jedes Ergebnis als günstig ansehen, dann muss ja E die ganze Menge Ω sein.

Und auch das kann man formal schreiben: Es P({ }) = 0 und P(Ω) = 1.

Betrachten wir schließlich unabhängige Ereignisse E₁ und E₂, also jeweils Ergebnisse, die als günstig angesehen werden, aber keine gemeinsamen Elemente haben. Dann müssen wir offensichtlich die einzelnen Wahrscheinlichkeiten addieren, um die Wahrscheinlichkeit von E₁ und E₂ zusammen zu bekommen.

Formal geschrieben: Es ist P(E₁∪E₂) = P(E₁) + P(E₂) falls E₁∩E₂ = { }

Sie sehen also, diese Charakteristika von Laplace-Wahrscheinlichkeiten leitet sich ohne Umwege über den gesunden Menschenverstand ab.

In der Mathematik sucht man dann nach einer formalen Ausdrucksweise. Nein, sicher nicht, um sich von der restlichen Welt abzugrenzen. Vielmehr geht es darum eine eindeutige Darstellung, die keine Zweifel daran aufkommen lässt, was sie aussagt. Sie wissen, unsere normale Sprache kann diesem Anspruch nicht gerecht werden.

Folie 10

Nun ist nicht jedes Zufallsexperiment ein Laplace-Experiment und Sie sehen hier ein Beispiel.

Wir drehen das hier abgebildete Glücksrad. Dann ist Ω = {1, 2, 3} und es ist außerdem sinnvoll anzunehmen: P(1) = ¼ , P(2) = ¼, P(3) = ½

Auch hier würde jede andere Festlegung nicht plausibel erscheinen.

Genauso würde man die Wahrscheinlichkeit, eine 1 oder eine 2 zu erzielen, durch

P(1) + P(2) = ¼ + ¼ = ½ berechnen.

Man kann nur 1 oder 2 oder 3 als Ergebnis haben, also ist P(Ω) = 1. Irgendwo wird der Zeiger schon stehenbleiben.

Eine 4 taucht nicht auf, die Wahrscheinlichkeit dafür ist Null. Und das gilt genauso für die 5, die 6 oder die 7 oder alle anderen Zahlen, die nicht auf dem Rad stehen. Das sind unmögliche Ereignisse.

Und wieder formalisieren wir das auf der folgenden Seite.

Folie 11

Es ist auch hier 0 ≤ P(E) ≤ 1 für alle Ereignisse E, d. h. die Wahrscheinlichkeit für jedes Ereignis E liegt zwischen 0 und 1.

Ebenso gilt P({ }) = 0 und P(Ω) = 1. Das unmögliche Ereignis hat die Wahrscheinlichkeit 0, das sichere Ereignis die Wahrscheinlichkeit 1.

Und schließlich ist P(E₁∪E₂) = P(E₁) + P(E₂) falls E₁∩E₂ = { }. Sie erinnern sich: Wenn das Glücksrad bei der 1 oder der 2 stehen bleibt, dann addieren sich die einzelnen Wahrscheinlichkeiten für 1 und für 2 für dieses zusammengesetzte Ereignis.

Folie 12

Wir wissen, dass es nicht zu jedem Zufallsexperiment theoretische Annahmen über den Ausgang gibt. Wir hatten das am Beispiel einer Reißzwecke betrachtet und sie 1000-mal geworfen. Sie fiel dabei 633-mal auf den Kopf und 367-mal auf die Seite.

Es ist also sinnvoll anzunehmen, dass

P(Kopf) = 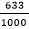und P(Seite) =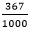

ist. Natürlich, hier kann sich die Annahme im nächsten Versuch oder mit einer neuen Sorte von Reißzwecken leicht ändern.

Bekommen wir das trotzdem in den Griff? Lassen Sie es uns versuchen.

Folie 13

Grundbegriffe sind hier die absolute und relative Häufigkeit.

Wird ein Zufallsexperiment mehrfach wiederholt, so tritt jedes Ereignis mit einer bestimmten Häufigkeit auf. Diese Zahl nennt man die absolute Häufigkeit.

Fällt also beispielsweise eine Reißzwecke beim 1000-maligen Werfen 633-mal auf den Kopf, so ist 633 die absolute Häufigkeit des Ereignisses „Kopf“.

Ganz allgemein: Tritt ein Ereignis A bei n Versuchen k-mal ein, so heißt h_n(A) = k/n die relative Häufigkeit des Ereignisses A in dieser Versuchsfolge.

Fällt eine Reißzwecke also beim 1000-maligen Werfen 633-mal auf den Kopf, so ist

h₁₀₀₀(Kopf) := 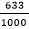= 0,633 = 63,3%

die relative Häufigkeit des Ereignisses „Kopf“.

Folie 14

Die relative Häufigkeit ist nun der Ausgangpunkt für eine Definition des Begriffs der Wahrscheinlichkeit, der sogenannten statistischen Wahrscheinlichkeit.

Die grundlegende Idee geht auf Richard von Mises zurück der von1883 bis 1953 lebte und sie 1919 erstmals veröffentlichte. Wir bestimmen bei einem Zufallsexperiment die relative Häufigkeit bei einer sehr großen Anzahl von Versuchen, was man als frequentistische Methode bezeichnet. Dabei stellen wir uns vor, wir könnten das Experiment „unendlich oft“ durchführen.

Die statistische Wahrscheinlichkeit eines Ereignisses A wird nun definiert als der Grenzwert der relativen Häufigkeit, wenn man das Experiment „unendlich oft“ ausführen würde:

Klingt gut, oder? Sieht auch wunderbar mathematisch aus, oder? Trotzdem gibt es Tücken, auf die wir nachher eingehen werden. Aber lassen Sie uns zunächst die vertraut gewordenen Eigenschaften betrachten. Ich verspreche Ihnen, es klappt auch dieses Mal.

Folie 15

Zunächst fällt die Reißzwecke beim Werfen auf die Seite oder auf den Kopf. Wir können wieder den möglichen Ereignissen eine Wahrscheinlichkeit zuordnen, auch wenn sie experimentell gewonnen wurde. In jedem Fall ist eine Zahl zwischen 0 und 1, wobei 0 das unmögliche Ereignis und 1 das Ereignis „entweder Kopf oder Seite“ charakterisiert.

Schon haben wir die beiden ersten Eigenschaften hübsch formal aufgeschrieben: Es ist 0 ≤ P(E) ≤ 1 für alle Ereignisse E, P({ }) = 0 und P(Ω) = 1.

Auch die dritte Eigenschaft erklärt sich von selbst. Wieder ist P(E₁∪E₂) = P(E₁) + P(E₂) falls E₁∩E₂ = { }.

Folie 16

Ich hatte schon angedeutet, dass der Begriff der statistischen Wahrscheinlichkeit nicht problemlos ist. Ein ganz großes Problem ist, dass wir ein Zufallsexperiment nicht unendlich oft durchführen können. Und für den endlichen Fall ist – das haben wir bereits gesehen – dem Zufall alles zuzutrauen.

Ein Beispiel: Am 18. August 1913 soll im Spielcasino von Monte Carlo die Kugel beim Roulette 26-mal hintereinander auf ein schwarzes Feld gefallen sein. Viele Menschen haben an diesem Tag viel Geld verloren, weil sie zu früh auf eine andere Farbe gesetzt hatten.

In der Konsequenz kann der Grenzwertbegriff so wie er in der statistischen Wahrscheinlichkeit verwendet wird, nicht die Präzision des Grenzwertbegriffs haben, wie man ihn aus der Analysis kennt. So etwas mag man in der Mathematik nicht und das war ein wichtiger Grund für die weitere Forschung in diesem Bereich.

Folie 17

Der Durchbruch gelang Andrei Nikolajewitsch Kolmogorow, der im Jahr 1933 ein Buch veröffentlichte, in dem er einen axiomatischen Wahrscheinlichkeitsbegriff vorschlug. Hier sind die Axiome – die Sie inzwischen eigentlich schon alle kennen. Aber der Reihe nach.

Nehmen wir an, dass die Menge Ω ein endlicher Ergebnisraum ist. Denken Sie sich hier ruhig die sechs Zahlen eines Würfels oder die zwei Möglichkeiten des Fallens einer der Reißzwecke. Nehmen wir nun an, P ist eine Abbildung, die jedem Ereignis eine reelle Zahl zuordnet. P soll also allen Teilmengen von Ω eine reelle Zahl zuordnen. Die Menge aller Teilmengen einer Menge ist ihre Potenzmenge und damit ist P eine Abbildung von der Potenzmenge P(Ω) in die Menge ℝ.

Diese Abbildung P hat einen spezifischen Namen. Wir nennen sie Wahrscheinlichkeitsverteilung genau dann, wenn die folgenden Axiome erfüllt sind:

1. P(A) ≥ 0 für alle A ∈ P(Ω).
2. P(Ω) = 1.
3. Für Ereignisse A, B ∈ P(Ω) mit A ∩ B = {} gilt:
   P(A ∪ B) = P(A) + P(B).

Nun ja, und diese Axiome hatten wir uns bereits erarbeitet. Beim Würfeln genauso wie beim Glücksrad oder der Reißzwecke, also bei Laplace-Experimenten und anderen Zufallsexperimenten.

Folie 18

Diese Axiome kann man treffend beschreiben. Das erste Axiom P(A) ≥ 0 für alle A ∈ P(Ω) bedeutet die Nicht-Negativität, denn P hat Werte, die größer oder gleich Null sind.

Das zweite Axiom liefert eine Normierung. Weil Ω alle Ergebnisse enthält, ist die Festlegung P(Ω) = 1 sinnvoll, da dann alle Ereignisse vernünftigerweise unter P einen Wert zwischen 0 und 1 annehmen sollten.

Und damit das sicher klappt, kommt als drittes Axiom die Additivität hinzu. Für die Ereignisse A, B ∈ P(Ω) mit A ∩ B = { } gilt: P(A ∪ B) = P(A) + P(B).

Sind diese Axiome nun wirklich geeignet? Das soll hier und jetzt nicht unsere Sorge sein. Wir verlassen uns an dieser Stelle auf die vielen Beispiele, die das plausibel machen.

Folie 19

Und nein, der axiomatische Wahrscheinlichkeitsbegriff sagt uns nichts darüber, wie die Sache mit den Reißzwecken auf lange Sicht ausgeht.

Aber er macht sie mathematisch krisensicher und ist Basis für Folgerungen und Berechnungen.

Lassen Sie uns ein Beispiel betrachten. Wir können aus den drei Axiomen ableiten, dass P({ }) = 0 ist.

Zunächst ist Ω ∩ { } = { }. Das ist ganz einfach aus den Regeln des Umgangs mit Mengen abzuleiten.

Wir wissen außerdem, dass P(Ω) = 1 ist, dass besagt das zweite Axiom.

Nun ist P(Ω ∪ { }) = P(Ω) + P({ }) wegen Axiom 3 und wir setzen zusammen:

Es ist also 1 = P(Ω) = P(Ω ∪ { }) = P(Ω) + P({ }) und somit P({ }) = 0.

Folie 20

Ging Ihnen das zu schnell? Keine Sorge. Ich habe hier den Beweis noch einmal Schritt für Schritt ausgeführt.

Die Form – Behauptungen links und Begründungen rechts habe ich aus dem angelsächsischen Raum übernommen. Dort spricht man dann vom „Beweis in zwei Spalten“. Machen Sie eine Pause, schauen Sie sich das im Detail an. Mathematik kann man einfach nicht nur durch Zuhören verstehen.

Folie 21

Und wenn Sie noch etwas üben möchten, dann könnten Sie vielleicht diesen Beweis ausführen:

Betrachten Sie ein Ereignis A und sein Gegenereignis „nicht A“. Beweisen Sie, dass P(A) + P(nicht A) = 1 ist.

Ich empfehle durchaus, diesen Beweis in zwei Spalten zu schreiben.

Folie 21a

Das ist die Lösung. Schauen Sie sich das einfach in Ruhe an.

Folie 22

Wir haben in dieser Folge drei Ideen des Wahrscheinlichkeitsbegriffs definiert. Zunächst basierte dies auf der relativen Häufigkeit eines Ereignisses in einem Laplace Experiment. Dann haben wir eine Idee diskutiert, die auf dem Gesetz der großen Zahlen beruht. Schließlich haben wir Kolmogorows Zugang vorgestellt, der auf Axiomen basiert. Sicherlich fanden Sie den einen Begriff spontan leichter zugänglich als den anderen. Ich denke aber, dass alle drei Ideen für den Mathematikunterricht sehr nützlich seien. Überlegen Sie sich doch einmal in welcher Situation welcher Begriff am besten geeignet ist und welche Vor- und Nachteile die behandelten Zugänge aufzeigen.

Folie 23

Das war es für heute. Haben Sie vielen Dank, dass Sie dabei waren. Ich freue mich auf Sie in der nächsten Folge.