Folie 0

Lassen Sie uns wieder über Mathematik reden. Herzlich willkommen zu dieser neuen Folge. Wir werden uns heute mit ein paar Grundbegriffen der Stochastik auseinandersetzen und sehen, wie man sie in einen handlungsorientierten Mathematikunterricht integrieren können. Wir werden uns dabei mit einfachen Daten aus einer leicht realisierbaren Erhebung beschäftigen.

Lassen Sie uns anfangen.

Folie 1

Stellen Sie sich vor, Sie planen eine Erhebung in der Schule. Und selbstverständlich eine, die eine Klasse größtenteils selbst durchführen und auswerten kann. Das Ziel ist dabei die Antwort auf diese zunächst sehr allgemein gestellte Frage:

Interessieren sich die Schülerinnen und Schüler für das Fach Mathematik? Ein Vergleich soll mit dem Fach Deutsch erfolgen.

Die Methode ist fachlich angemessen: Es wird ein Fragebogen entworfen, der dann passend ausgewertet werden kann.

Folie 2

Was gehört in den Fragebogen? Nun, man könnte zum Beispiel nach der Klassenstufe, dem Alter, dem Geschlecht, dem Interesse an diesen und anderen Fächern, nach der Motivation, sich in der Freizeit mit den jeweiligen fachlichen Inhalten zu beschäftigen, dem Lieblingsfach oder den Noten (z. B. in der letzten Klausur) fragen.

Bei jeder einzelnen Frage gilt es, vorab zwei wesentliche Aspekte zu klären.

Zum einen muss man sich sicher sein, warum man eine bestimmte Frage stellt. Dieser Aspekt ist nicht nur eine Propädeutik für hypothesengeleitetes Arbeiten, sondern gibt auch die Möglichkeit, den Umgang mit Daten im Hinblick auf den Datenschutz anzusprechen.

Zum anderen muss man sich das wie überlegen. Erhebt man das Alter in Jahren oder Jahren und Monaten? Welchen Grad der Feinheit kann man sinnvoll nutzen? Wird das Interesse an einem Fach beispielsweise auf einer vier- oder fünfstufigen Skala abgebildet? Natürlich ist das wie mit dem warum eng verbunden.

Folie 3

Die Daten, die hier erhoben werden, sind recht unterschiedlich. Daten wie das Geschlecht oder das Lieblingsfach bezeichnet man als qualitative Daten. Man kodiert mit qualitativen Merkmalen. Ganz einfach gesprochen – und das darf man im Unterricht in vielen Situationen – sind es zumeist Daten, mit denen man nicht sinnvoll rechnen kann.

Folie 4

Daten wie die Klassenstufe, das Alter oder die Note in der letzten Klausur sind quantitative Daten, die mit Zahlen kodiert werden. Entsprechend kann man sie in eine Reihenfolge bringen und beispielsweise das mittlere Alter eine Stichprobe bestimmen oder die Durchschnittsnoten von Klausuren berechnen.

Aber Vorsicht, auch diese Werte müssen im Kontext einer Befragung sinnvoll interpretiert werden. Eine bessere Note in einer Klausur gilt als erstrebenswert, ein höheres oder niedrigeres Alter ist nicht unbedingt ein Qualitätsmerkmal und kann vor allem nicht außerhalb eines spezifischen Kontextes bewertet werden.

Folie 5

Und was machen wir schließlich mit dem Interesse am Fach oder der Motivation, sich in der Freizeit mit den fachlichen Inhalten zu beschäftigen? Auch das sind qualitative Daten, wenn man eine qualitative Ausprägung etwa von sehr hoch bis sehr niedrig erhebt.

Folie 6

Wichtig ist aber gerade hier eine weitere Unterscheidung, nämlich die in ordinale und nominale Daten.

Alter, Klassenstufe, Noten sind Beispiele für ordinale Daten, denn man kann sie in eine sinnvolle Reihenfolge bringen. Geschlecht und Lieblingsfach sind Beispiele für nominale Daten, denn hier gibt es keine sinnvolle Reihenfolge.

Man kann allerdings auch Daten wie Interesse und Motivation in eine Rangordnung bringen. Das macht man, in dem man etwa mit Zahlen zwischen 1 und 5 je nach Höhe der Ausprägung kodiert.

Dabei ist allerdings zu beachten, dass sich eine hohe von einer mittleren Motivation noch schlechter abgrenzen lässt, als die Schulnote 2 von der Schulnote 3. Es ist wichtig zu wissen, dass die Abstände zwischen den einzelnen Ausprägungen nicht unbedingt gleich sind.

Trotzdem wird mit solchen Zahlen gerechnet, trotzdem werden Mittelwerte bestimmt und das ist auch völlig legitim. Es kommt vor allem darauf an, die Schwächen einer Kodierung bei der Interpretation der Daten zu berücksichtigen.

Folie 7

Lassen Sie uns zu den Begriffen gehen. Wir nehmen an, alle Vorarbeiten sind abgeschlossen und die Befragung wurde durchgeführt.

Einen geeigneten Fragebogen haben 882 Schülerinnen und Schüler der Marie-Curie-Schule in den Klassen 5 bis 10 ausgefüllt. Die Ergebnisse bestätigen die Vermutung: Es gibt mehr Schülerinnen und Schüler, die Deutsch als Lieblingsfach wählen, als solche, die Mathematik nennen. Die anderen Fächer landen – vielleicht etwas überraschend – insgesamt auf dem dritten Platz.

In absoluten Zahlen nennen 441 Schülerinnen und Schüler Deutsch als ihr Lieblingsfach, für 312 ist es Mathematik und für 129 ein anderes Fach. Man bekommt so ganz einfach einen wichtigen Grundbegriff der Statistik, nämlich die absolute Häufigkeit. Wenn es um die Frage nach dem Lieblingsfach und die Antwort „Mathematik“ geht, dann ist die absolute Häufigkeit 312.

Folie 8

Nun sind 312 von 882 sicherlich etwas anderes als 312 von 1.000.000. Was können wir mit diesen absoluten Werten anfangen? Nun ja, es bietet sich an, sie auf die Grundgesamtheit zu beziehen. Man berechnet daher die relative Häufigkeit als Quotient aus absoluter Häufigkeit und Größe der Grundgesamtheit.

Und dann überlegt man sich sinnvollerweise noch eine gute Darstellung, die hier beispielsweise ein Kreisdiagramm sein kann.

Die Daten haben sich nicht geändert, sie sind so aber leichter zu bewerten. Genau die Hälfte der Schülerinnen und Schüler hat Deutsch als Lieblingsfach genannt, gut ein Drittel sprach sich für die Mathematik aus. Und diese Werte sieht man im Kreisdiagramm sofort.

Folie 9

In einer weiteren Frage wurde das Interesse der Schülerinnen und Schüler an den Fächern Deutsch und Mathematik erhoben. Dabei wurde eine so genannte Likert-Skala verwendet, die von 5 („sehr hohes Interesse“) bis zu 1 („gar kein Interesse“) recht. Auch hier sieht man sich zunächst die absoluten Zahlen an, die Urliste – und diesen Begriff haben wir schon früher einmal verwendet.

Folie 10

Aber auch hier ist die Aussagekraft der absoluten Häufigkeiten begrenzt. Wir suchen also wieder eine geeignete, auf einen Blick aussagekräftige Darstellung. Hier könnte das etwa ein Säulendiagramm sein.

Die Werte für beide Fächer kann man nett nebeneinander eintragen und liest so – zumindest qualitativ – die Unterschiede leicht ab. Deutsch hat Höchstwerte bei hohem und mittlerem Interesse, Mathematik zwar auch, aber die Säule beim hohen Interesse ist deutlich niedriger.

Folie 11

Mit aller Vorsicht – das haben wir vorhin schon angesprochen – bestimmen wir eine mittlere Ausprägung und berechnen das arithmetische Mittel. Dazu gewichtet man schlicht die einzelnen Ausprägungen, also die einzelnen Werte für das Interesse. Man dividiert dann durch die Größe der Stichprobe, also die Anzahl aller befragten Schülerinnen und Schüler.

Ein sehr hohes Interesse an Mathematik haben 149 Schülerinnen und Schüler angekreuzt, also geht dieser Wert mit 5 • 149 in die Berechnung ein. Insgesamt kommt man auf ( 5 •149 + 4 • 206 + 3 • 256 + 2 • 174 + 1 • 97 ) : 882 und das ist gerundet 3,15.

Folie 12

Für das Fach Deutsch liegt der Wert bei 3,48, also – und wie aus einem ersten Blick auf die Daten erwartet – höher. Schade, da haben sich die Erwartungen, die man vor der Erhebung hatte, ebenfalls bestätigt.

Natürlich könnte man sich nun noch fragen, ob der Unterschied zwischen den beiden Mittelwerten wirklich aussagekräftig – oder mit dem Fachbegriff gesprochen – signifikant ist.

Die Antwort verschieben wir auf eine spätere Folge.

Folie 13

Aber lassen Sie uns weitersehen, was auf einem eher einfachen Niveau noch interessant sein könnte.

Wir betrachten die Datenreihe erneut und stellen fest, dass mehr als die Hälfte der Schülerinnen mindestens hohes Interesse am Fach Deutsch hat.  Es ist

198 + 263 = 461 und das ist größer als 882 : 2 = 441.

Übrigens würde für die folgenden Betrachtungen die Beziehung „größer oder gleich“ genügen und deswegen sehen Sie das hier in der schriftlichen Fassung.

Für die Mathematik sieht es anders aus, aber immerhin hat mehr als die Hälfte der Schülerinnen ein mindestens mittleres Interesse. Es ist

149 + 206  + 256 = 611, was größer als 882 : 2 = 441 ist

aber

149 + 206  = 355 und das ist kleiner als 882 : 2 = 441

Folie 14

In der Folge bekommt man einen neuen Begriff:

Wir betrachten eine Datenreihe und den Wert, der – locker gesprochen – auf der „Hälfte“ liegt, sodass sich vor und hinter diesem Wert genau die Hälfte der Daten befinden. Dieser Wert heißt Median.

Und wenn es gar keine solche „Mitte“ gibt, weil wir eine gerade Anzahl von Werten haben? Kein Problem, dann ist der Median das arithmetische Mittel der beiden mittleren Werte.

Im Beispiel ist der Median für das Interesse an der Mathematik = 3 und der Median für das Interesse an Deutsch = 4. Auch da liegt das Fach Deutsch also vorne.

Folie 15

Ist es nicht überflüssig, einen weiteren Mittelwert einzuführen, wenn es eh immer auf dasselbe hinausläuft? Klar, wenn es dann so wäre. Aber es muss nicht so sein und das sollen weitere Daten aus der Umfrage zeigen.

Dieses Mal geht es um die Noten in der letzten Klausur bei 27 Schülerinnen und Schülern der Klasse 8a und 29 Schülerinnen und Schülern der Klasse 8b. Hier sehen Sie die absoluten Zahlen der einzelnen Noten.

Folie 16

Berechnen wir arithmetisches Mittel und Median, dann ist das arithmetische Mittel mit m = 3,3 in beiden Klassen gleich. Der Median unterschiedet sich allerdings um eine Note und liegt bei 4 in der 8a und 3 in der 8b.

Folie 17

Schauen wir uns das noch einmal im Säulendiagramm an. Ganz offensichtlich zeigt sich in den beiden Klassen eine sehr unterschiedliche Häufigkeitsverteilung. In der Klasse 8a sind Schülerinnen und Schüler mit den richtig schlechten Noten 5 und 6 kaum vertreten, die Note 4 wurde ganz häufig vergeben und die besseren Noten 1, 2 und 3 sind zwar zu sehen, aber eben auch in geringeren Zahlen.

In der Klasse 8b gibt es eine Spitze bei den Noten 2 und 3, ansonsten wird das ganze Notenspektrum ausgenutzt. Dies führt zum Unterschied im Median bei einem identischen arithmetischen Mittel.

Folie 18

Offensichtlich sind Mittelwerte also nicht immer hinreichend aussagekräftig, sondern es kommt auch auf die Streuung der Daten an. Man interessiert sich entsprechend dafür, wie Werte von einem Mittelwert abweichen.

Betrachten wir ein solches „Abweichungsmaß“.

Folie 19

Das arithmetische Mittel war in beiden Klassen 3,3. Schauen wir uns an, wie die einzelnen gemessenen Werte von diesem arithmetischen Mittel abweichen.

Dazu bildet man einfach die Differenzen. 3,3 – 1 = 2,3, 3,3 – 2 = 1,3, 3,3 – 3 = 0,3 usw.

Folie 20

Und nun gewichten wir diese Unterschiede. Wir rechnen für die Klasse 8a

2 • 2,3 + 4 • 1,3 + 6 • 0,3 + 14 • 0,7 + 1 • 1,7 + 0 • 2,7 = 23,1

Folie 21

Und für die Klasse 8b

2 • 2,3 + 8 • 1,3 + 8 • 0,3 + 5 • 0,7 + 3 • 1,7 + 3 • 2,7 = 34,1

Folie 22

Man kann daraus eine mittlere Abweichung berechnen, wenn man jeweils durch die Anzahl der Schülerinnen und Schüler teilt.

.

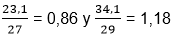Diese schlichten Rechnungen geben schon ein Gefühl für die Unterschiede. In Klasse 8a weichen die gemessenen Noten im Mittel weniger stark vom arithmetischen Mittel ab als in der Klasse 8b.

Folie 23

Soweit das Prinzip, in der Praxis macht man es etwas anders. Nehmen wir an, wir gehen von n Zahlen aus. Dann bildet man die Differenz zwischen einem einzelnen Wert und dem arithmetischen Mittel und quadriert diese Zahl. Der Grund ist einfach, denn so wird aus einer positiven wie aus einer negativen Differenz eine positive Zahl und man hat keinen Ärger mit dem Vorzeichen. Das macht man mit jedem gemessenen Wert und bildet schließlich die Summe über alle diese n Zahlen.

Dann wird dividiert, allerdings in der Regel nicht durch n, sondern durch n-1. Diese Zahl nennt man empirische Varianz oder nur Varianz. Und wenn man daraus die Wurzel zieht, dann bekommt man die Standardabweichung.

Man geht also im Beispiel von 2,3² = 5,29; 1,3² = 1,69; 0,3² = 0,09; 0,7² = 0,49; 1,7² = 2,89;   2,7² = 7,29 aus.

Folie 24

Wir gewichten nun die Unterschiede mit diesen quadratischen Termen zunächst für die Klasse 8a. Zwei Schülerinnen und Schüler gaben eine 1 als Klausurnote an, also geht 5,29 mit dem Faktor 2 in diese Summe ein. Acht Schülerinnen und Schüler gaben die 2 an, also geht 1,69 mit dem Faktor 8 in diese Summe ein. Und so geht es weiter bis zur Note 6, die niemand in der letzten Klausur hatte, sodass 7,29 mit 0 multipliziert wird.

Aufsummiert gibt das 27,63, teilen durch 26 ergibt 1,063 und die Wurzel daraus ist 1,03. Also ist die Standardabweisung Sigma = 1,03.

Für die Klasse 8b geht es genauso und wir bekommen Sigma = 1,44

Folie 25

Ganz offensichtlich streuen die gemessenen Werte in der Klasse 8b viel stärker als in der 8a. Das kann man auch qualitativ begründen.

Mit der Standardabweichung Sigma hat man dafür nun ein zuverlässiges Maß:

Ein Tipp: Rechnen Sie ein solches Beispiel einmal selber nach. Dadurch wird viel anschaulicher, warum dieses Vorgehen sinnvoll ist. Insbesondere sieht man, warum große Unterschiede zum Mittelwert sehr ins Gewicht fallen und kleinere Unterschiede eher vernachlässigt werden.

Und ja, man könnte es sicher anders machen. Dieses Vorgehen ist nicht zwingend, es gibt durchaus andere Maße für die Streuung. Die würden Unterschiede dann auf eine andere Art und Weise eingehen lassen, also anders vernachlässigen oder anders betonen. Diese Freiheit gehört sicherlich für manche Schülerinnen und Schüler eher zu den Problemen mit der Stochastik.

Folie 26

Das war es für heute, vielleicht keine ganz einfache Folge. Ich hoffe es hat Ihnen trotzdem etwas Spaß gemacht. Haben Sie vielen Dank, dass Sie dabei waren. Ich freue mich auf Sie beim nächsten Mal.