24 Einmal bestimmt, immer gültig? Die Wahrscheinlichkeit und das Ziegenproblem.

Folie 0

Herzlich willkommen zu dieser neuen Folge. Wieder einmal reden wir über Mathematik. Dabei geht es heute um eine Ziege und ein Problem, das sie bereiten kann. Naja, und dann auch um die bedingte Wahrscheinlichkeit.

Folie 1

Mehrstufige Zufallsexperimente und bedingte Wahrscheinlichkeiten – damit haben wir uns schon in der vorigen Folge beschäftigt. So ganz kompliziert ist es nicht geworden, denn wir haben uns auf zweistufige Zufallsexperimente beschränkt. Doch selbstverständlich geht es auch komplexer. Aber keine Angst, es wird wirklich nur ein ganz klein wenig komplizierter.

Folie 2

Wir beginnen mit einem ganz einfachen Fall, den man auch gut praktisch durchführen kann. Wir werfen dreimal eine Münze und betrachten, mit welcher Wahrscheinlichkeit genau zweimal „Zahl“ oben liegt.

Das ist rechnerisch eigentlich klar.

Es ist P(Zahl) = P(Kopf) = 1/2. Entsprechend ist die Wahrscheinlichkeit für eine bestimmte Folge von Kopf und Zahl also  ³ = 1/8.

Insgesamt gibt es acht Möglichkeiten. Wir überlegen, wie viele von ihnen „günstig“ sind.

Folie 3

Hier bietet sich ein Baumdiagramm an, denn da kann man – zumindest theoretisch – jede beliebige Anzahl von Stufen abtragen. Und wir sehen auch problemlos das Ergebnis. Von den acht möglichen Fällen sind es drei, bei denen zweimal die Zahl oben liegt. Sie sind hier mit einem grünen Punkt markiert.

Folie 4

Nun muss man manchmal Bedingungen berücksichtigen und auch dafür betrachten wir ein Beispiel.

Emilia ist eine Nachbarin von Anna und Leo. Ihre Katze hat vier Junge bekommen.

Leo weiß, dass ein männliches Tier dabei ist. Anna erzählt, dass sie sogar zwei männliche Kätzchen gesehen hat. Ob es auch weiblichen Nachwuchs gibt? Beide denken nach – und das zunächst einmal getrennt voneinander.

Folie 5

Leo überlegt, dass es prinzipiell fünf Möglichkeiten gibt. Es gibt kein männliches Kätzchen oder eines oder zwei oder drei oder vier – davon kommt eine Möglichkeit allerdings nach seinen Informationen nicht in Frage, denn er weiß ja, dass mindestens eines der Kätzchen männlich ist. Es bleiben also vier Möglichkeiten, bei denen zumindest ein männliches Tier dabei ist. Bei einer dieser Möglichkeiten sind allerdings alle Tiere männlich, somit gibt es drei günstige Fälle und eine Wahrscheinlichkeit von ¾ für mindestens ein weibliches Kätzchen.

Anna hat mehr Informationen und so kann sie von den fünf Möglichkeiten gleich zwei ausschließen. Von den verbleibenden drei Möglichkeiten sind zwei günstig: Sie kommt auf die niedrigere Wahrscheinlichkeit von 2/3 für ein weibliches Kätzchen im Wurf.

Folie 6

Also offensichtlich ist die Beurteilung der Wahrscheinlichkeit eines Ereignisses nicht unbedingt eine feste Größe. Sie kann vielmehr von unterschiedlichen Informationen abhängen. Und genau darum geht es im Ziegenproblem.

Folie 7

Stellen Sie sich vor, Sie dürfen ins Fernsehen. In einer Spielshow lockt der Hauptgewinn, ein nagelneues, wunderschönes Auto, und davon trennt Sie nur eine einzige Frage. Allerdings brauchen Sie zur Beantwortung dieser Frage etwas Glück. Naja, und auch mathematisches Wissen kann nicht wirklich schaden.

Folie 8

Und das ist die Situation

Sie stehen vor drei -natürlich verschlossenen – Türen. Hinter einer verbirgt sich das Auto, das Sie sehr gerne hätten. Hinter den beiden anderen verbergen sich Ziegen. Sie dürfen eine Tür auswählen und auf Ihr Glück vertrauen.

Nehmen wir an, Sie entscheiden sich für Tür 1. Nun öffnet der Moderator – und er kennt des Rätsels Lösung – allerdings nicht diese Tür, sondern Tür 3. Dahinter ist eine Ziege. Er fragt Sie, ob Sie bei Ihrer ursprünglichen Wahl bleiben oder ob Sie lieber Tür 2 öffnen lassen wollen.

Was denken Sie? Ist es nicht ganz egal, welche der beiden Türen Sie wählen? Oder gibt es bei einer der beiden Türen eine höhere Chance auf einen Gewinn?

Geben Sie einen Tipp ab.

Folie 9

Wir schauen uns die Situation – wie so oft – einmal ganz genau an. Im ersten Schritt wählen Sie beliebig eine Tür. Die Wahrscheinlichkeit, dass dahinter das Auto ist, also die Chance für einen Gewinn ist ganz offensichtlich 1/3. Es gibt genau einen günstigen von drei möglichen Fällen.

Folie 10

Im zweiten Schritt kommt nun der Moderator hinzu. Er öffnet Tür 3. Die Spannung wächst. Was ist dahinter?

Folie 11

Und dahinter ist eine Ziege zu sehen. Wo ist also das Auto?

Nehmen wir an, Sie hatten sich für Tür 1 entschieden und überlegen nun, ob ein Wechsel günstig ist. Es gibt ganz klar noch immer diese drei Türen:

Aber nun ist der Gewinn entweder hinter Tür 1 oder der Gewinn ist hinter Tür 2, denn hinter Tür 3 ist offensichtlich eine Ziege

Folie 12

Spielen wir doch einmal die Situationen durch.

Nehmen wir an, der Gewinn ist hinter Tür 1. Dann haben Sie schlicht Pech gehabt, wenn Sie wechseln.

Angenommen aber, der Gewinn ist hinter Tür 2. Dann kann der Moderator Tür 1 nicht öffnen, weil Sie das vorgeschlagen haben, und Tür 2 nicht, weil dort der Gewinn ist. Er öffnet Tür 3, ein Wechsel zu Tür 2 ist günstig für Sie.

Angenommen, der Gewinn ist hinter Tür 3. Dann kann der Moderator Tür 1 nicht öffnen, weil Sie das vorgeschlagen haben, und Tür 3 nicht, weil dort der Gewinn ist. Er öffnet Tür 2, ein Wechsel zu Tür 3 ist günstig für Sie.

Mit anderen Worten: In zwei von drei Situationen ist der Wechsel günstig für Sie und Ihre Gewinnwahrscheinlichkeit steigt auf 2/3.

Folie 13

Und nun ganz systematisch. Es geht um diese Ereignisse:

G_i := Der Gewinn ist hinter Tür i (für i = 1,2,3).

M_i := Der Moderator öffnet Tür i (für i = 1,2,3).

Zu Beginn ist für Sie eigentlich alles ganz einfach und erfordert kein großes Nachdenken. Sie haben keine Informationen und deswegen ist P(G₁) = P(G₂) = P(G₃) = 1/3.

Folie 14

Nun haben Sie sich für Tür 1 entschieden und wir nehmen an, der Moderator hat Tür 3 geöffnet.

Wir suchen daher P(G₁|M₃) und P(G₂|M₃).

Das erfordert nun etwas Arbeit vorher. Wir überlegen, mit welcher Wahrscheinlichkeit der Moderator Tür 2 bzw. Tür 3 öffnet. Und klar, wir beachten dabei, dass Sie Tür 1 gewählt haben.

Folie 15

Sie haben sich für Tür 1 entschieden, der Moderator hat Tür 3 geöffnet. Wir haben gerade eben die Möglichkeiten in diesem Fall gesehen. Hinterfragen wir sie noch einmal.

Warum ist P(M₃|G₁) = ½?

Sie sagen „Tür 1“, das wäre in diesem Fall auch der Gewinn. Der Moderator hat beim Öffnen die freie Wahl zwischen den Türen 2 und 3. Die Wahrscheinlichkeit, dass er Tür 3 wählt, ist also ½.

Warum ist P(M₃|G₂) = 1?

Sie sagen „Tür 1“, dahinter ist eine Ziege. Der Moderator kann nun Tür 1 (Ihre Wahl) und Tür 2 nicht öffnen (Gewinn!!!). Er wählt mit Sicherheit Tür 3.

Warum ist P(M₃|G₃) = 0?

Naja, das wäre wirklich gegen den Sinn des Spiels.

Folie 16

Wir nehmen – und das ist ein wichtiges Detail – die Sicht des Moderators ein. Hier ist die Übersicht, die Zahlen kennen sie bereits.

Folie 17

Sie erinnern sich an die Formel von Bayes?

Es gibt eine Erweiterung, die nun auch eine formale Lösung des Problems zulässt (und die Begründung findet man in der einschlägigen Literatur). Man braucht

                             

                  P(M₃|G₂) = 1                     P(M₃|G₃) = 0

und rechnet

 

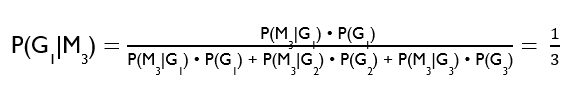
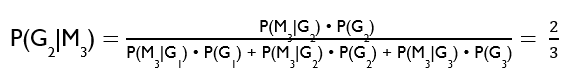
Noch einmal anders ausgedrückt. Die Wahrscheinlichkeit für Tür 1 war vorher ein Drittel und ändert sich nicht. Durch die zusätzliche Information steigt die Wahrscheinlichkeit für Tür 2.

Folie 18

Was haben wir heute gemacht?

Irgendwie schon wieder etwas über unsere schlechte Intuition für stochastische Zusammenhänge gelernt. Aber das war nicht alles. Wir haben gesehen, dass der jeweilige Blickwinkel eine Rolle spielt.

• Beim Ziegenproblem ist zentral für die Beurteilung, dass der Moderator die richtige Lösung kennt.
• Auch bei den jungen Katzen waren es die konkreten Informationen, die Einfluss auf die Bestimmung der Wahrscheinlichkeiten hatten.

Fazit: Es geht nicht primär um Formeln und das Rechnen, sondern zunächst um die sinnvolle Interpretation einer stochastischen Situation.

Folie 19

Danke fürs Zuhören, das war heute nicht einfach. Vielleicht tröstet es Sie, dass es vor einiger Zeit heftige Diskussionen um das Ziegenproblem und seine korrekte Lösung gab und auch ausgewachsene Mathematiker oder Mathematikerinnen dabei falsch lagen. Bis zum nächsten Mal, ich freue mich auf Sie.