26 Die Spielbank gewinnt immer: Zufallsgrößen.

 

Folie 0

Die Anfänge der Wahrscheinlichkeitsrechnung waren stark durch das Glücksspiel bestimmt, was zunächst ja nicht für den allerbesten Ruf dieses Teilgebiets der Mathematik gesorgt hat. Wir haben entsprechend im Rahmen dieser Folgen zu Stochastik immer wieder versucht, den Blick auf andere und meist auch interessantere Anwendungen zu lenken.

Heute gibt es eine Ausnahme. Beim neuen Thema der Zufallsgrößen bietet es sich tatsächlich an darüber nachzudenken, warum zwar schon viele Menschen beim Glücksspiel Geld verloren haben, vom Zusammenbruch einer Spielbank aber eher selten – wenn überhaupt – berichtet wird.

Folie 1

Zufallsgrößen – wir haben den Begriff gerade schon verwendet – sind ganz einfach Funktionen.

Aber worum handelt es sich genau und was steckt hinter diesem Typ von Funktionen? Lassen Sie uns das Schritt für Schritt herausarbeiten.

Es geht einmal wieder um die Betrachtung und Einordnung von Situationen, bei denen der Zufall eine Rolle spielt.

Folie 2

Ich hatte es ja schon gesagt, heute soll das Glücksspiel eine Rolle spielen. Kennen Sie etwa das Spiel „Chuck-a-luck“? Es funktioniert denkbar einfach.

Sie setzen 1 Euro ein und spielen gegen die Bank. Sie wählen eine Augenzahl zwischen 1 und 6. Dann werden drei Würfel geworfen.

Zeigt mindestens ein Würfel die von Ihnen gewählte Augenzahl, so bekommen Sie den Einsatz zurück und zusätzlich 1 Euro pro Würfel mit der gewählten Augenzahl.

Erscheint Ihre Zahl nicht, so verfällt der Einsatz.

Folie 3

Die zentrale Frage für Sie ist: Was ändert sich in Ihrem Portemonnaie?

Das kann man über eine Funktion beschreiben. Man kann jedem Ergebnis des Zufallsexperiments „Dreifacher Würfelwurf“ eindeutig eine Zahl aus der Menge {-1; 1; 2; 3} zuordnen, denn entweder verliert man einen Euro, oder aber man erhält 1 bzw. 2 bzw. 3 Euro.

Nehmen wir an, der Sie haben sich für die „6“ entschieden.

Dann Es fehlt ein Euro im Portemonnaie bei allen Dreierkombinationen ohne eine 6. Und drei Euro mehr sind es nur beim Tripel (6,6,6).

Folie 4

Allgemein wird jedem Tripel aus drei Zahlen (und das sind die Würfe) ein Gewinn bzw. Verlust zugeordnet. Diese Funktion hat die Definitionsmenge
D = { (a,b,c) | a, b, c {1,2,3,4,5,6} } und die Wertemenge Ω = { -1, 1, 2, 3 } .

Allen 6³ = 216 Tripeln aus ganzen Zahlen zwischen 1 und 6 wird eine der Zahlen aus W zugeordnet.

Folie 5

Spielen wir es einmal konkret durch. Angenommen, ein Spieler wählt eine „6“. Dann fehlt bei allen Kombinationen von drei Zahlen zwischen 1 und 6 ohne eine „6“ am Ende ein Euro im Portemonnaie. Das sind gerade alle Kombinationen von drei Zahlen zwischen 1 und 5.

Sie sehen alle Möglichkeiten hier aufgelistet.

Und noch einmal, drei Euro gibt es von den 216 Fällen nur in einem einzigen Fall.

Folie 6

Definieren wir den Begriff.

Sei W ein endlicher Ergebnisraum. Dann heißt jede Funktion X von der Menge Ω in die Menge der reellen Zahlen (und ja, in der Realität geht es zumeist in eine sinnvolle Teilmenge)

eine Zufallsgröße (oder Zufallsvariable) auf Ω. Jedem ω aus Ω wird also eindeutig eine reelle Zahl X(ω) zugeordnet.

Ordnet man jedem möglichen Wert der Zufallsgröße die Wahrscheinlichkeit zu, mit der sie diesen Wert annimmt, so erhält man die Wahrscheinlichkeitsverteilung der Zufallsgröße.

Mit diesen Begriffen schauen wir noch einmal auf das Beispiel.

Folie 7

Im Beispiel Chuck-a-luck ist die Definitionsmenge der Zufallsgröße

Ω =  {(a,b,c) | a, b, c und 1 ≤ a,b,c ≤ 6}

und ihre Wertemenge

W =  {-1, 1, 2, 3} .

Und wie sieht es mit den Wahrscheinlichkeiten für die einzelnen Ergebnisse und folglich mit der Wahrscheinlichkeitsverteilung aus?

Folie 8

Wir müssen also sehen, wie groß

          P(X = -1)

          P(X =  1)

          P(X =  2)

          P(X =  3)

Damit kann man bestimmen, ob sich dieses Glücksspiel für die Spielerinnen und Spieler lohnt.

Folie 9

Man kann die Wahrscheinlichkeiten leicht bestimmen, hier helfen die Regeln der Kombinatorik. Es gilt einfach, die günstigen und die möglichen Fälle zu bestimmen. Insgesamt gibt es 6³ = 216 Möglichkeiten für Dreierkombinationen. Davon enthalten 5³ = 125 keine „6“. Wirft man einmal eine „6“ und zweimal eine andere Zahl, dann gibt es dafür 3 x 5² = 75 Möglichkeiten, denn die anderen Zahlen können an erster und zweiter, erster und dritter oder zweiter und dritter Stelle geworfen werden. Wirft man zweimal eine „6“ und einmal eine andere Zahl, dann gibt es 2 dafür 3 x 5 = 15 Möglichkeiten. Die andere Zahl kann ja als erste, als zweite oder als dritte geworfen werden. Und schließlich tritt die Kombination aus dreimal „6“ genau einmal auf.

Also ist

Folie 10

Nutzt man zur Darstellung eine Tabelle, dann sieht man die Wahrscheinlichkeitsverteilung auf einen Blick. In der ersten Zeile stehen die möglichen Gewinne, in der zweiten Zeile die dazu gehörenden Wahrscheinlichkeiten.

Folie 11

Mit diesen Zahlen kann man nun arbeiten und sich überlegen, was passiert, wenn man ausdauernd spielt. Macht man das, dann wird man auf lange Sicht in

125 von 216 Fällen 1 Euro verlieren

  75 von 216 Fällen 1 Euro gewinnen

  15 von 216 Fällen 2 Euro gewinnen

    1 von 216 Fällen 3 Euro gewinnen

Mit diesen Werten könnte man „gewichten“ und so einen „mittleren Gewinn“ (oder ggf. eben auch mittleren Verlust) pro Spiel bestimmen.

Folie 12

Sie sehen es hier. Wir haben den Verlust von 1 Euro bzw. die möglichen Gewinne mit der jeweiligen Wahrscheinlichkeit multipliziert und darüber die Summe gebildet. Das Ergebnis ist - oder rund -0,08. Wir nennen es „Erwartungswert“.

Es ist nicht schwer zu erkennen, dass es zwar einen kleinen, aber dennoch einen Verlust auf Seiten der Spielerin oder des Spielers gibt. Und dieser Verlust beträgt pro Spiel im Mittel 8 Cent.

Folie 13

Der Erwartungswert einer Zufallsgröße X ist die Summe aller angenommenen reellen Werte, die jeweils mit ihrer Wahrscheinlichkeit multipliziert wurden:

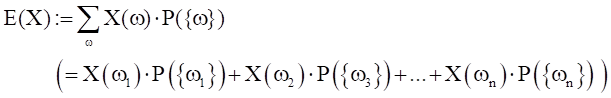
Der Erwartungswert ist also so etwas wie der mittlere Wert der Zufallsgröße pro Versuch auf lange Sicht.

Folie 14

Noch einmal konkret.

Ist Chuck-a-luck ein faires Spiel? Ganz offensichtlich müsste bei einem fairen Spiel E(X) = 0 sein. Wir haben es berechnet, E(X) < 0.

Bei sehr häufiger Wiederholung wird man einen durchschnittlichen Verlust von etwa 8 Cent pro Spiel erwarten und das bedeutet, dass es kein faires Spiel ist (was allerdings auch nicht wirklich überrascht).

Folie 15

Man kann den Erwartungswert und die notwendigen Berechnungen in diesem Fall mit einer kleinen Definitionsmenge sehr schön veranschaulichen.

Stellen Sie sich einen Balken vor, der wie ein Zahlenstrahl beschriftet ist. An den Stellen -1, 1, 2 und 3 befinden sich Körper mit den Massen 125/216, 75/216, 15/216 und 1/216. Dann kann man den Erwartungswert als „Schwerpunkt“ definieren. Unterstützt man den Balken hier, dann befindet sich der Balken im Gleichgewicht.

Folie 16

Lassen Sie uns ein weiteres Beispiel betrachten. Wir bleiben dabei im Kontext des Glücksspiels.

Haben Sie schon einmal das klassische Roulette gespielt? Eine Kugel rollt und trifft (zumindest in der europäischen Variante) eine von 37 Zahlen, von denen 18 einen roten, 18 einen schwarzen und eine einen grünen Hintergrund hat. Eine einfache Möglichkeit des Wettens: Man setzt auf ROT oder SCHWARZ. Kommt die gesetzte Farbe, ist der Gewinn der doppelte Einsatz. Ansonsten ist der Einsatz verloren.

Klingt gut, oder? Ein faires Spiel? Rechnen Sie es nach und setzen Sie wieder 1 Euro.

Folie 17

Man kann sofort ausschließen, dass es sich um ein faires Spiel handelt.

Von 37 Möglichkeiten sind nur 18 – und somit weniger als die Hälfte – günstige Fälle. Das kann entsprechend nur für die Spielbank gut ausgehen.

Wir rechnen trotzdem: In 18 von 37 Fällen gewinnt man 1 Euro, in 19 von 37 verliert man einen Euro. Somit ist

E(X)

 

 

Folie 18

Und nun machen Sie eine Spielbank auf. Die soliden Mathematikkenntnisse sollten sich ja auch einmal finanziell auszahlen.

Sie bieten ein Spiel an, bei dem der Einsatz einmal wieder 1 Euro ist.

So geht es: Es wird mit zwei Würfeln geworfen. Der Einsatz ist verloren, wenn darunter keine „6“ ist. Wie könnte der Gewinn bei einmal oder zweimal „6“ aussehen, sodass Sie nicht im Minus landen und das Spiel nicht allzu unfair ist?

Folie 19

So sieht es formal, übersichtlich und in Form einer Tabelle aus. Der Wert „-1“ ist klar, Sie können ja schlecht ihre Kunden mehr als den Einsatz verlieren lassen. Gesucht sind die Gewinne m und n, wenn einmal bzw. zweimal eine „6“ geworfen wird.

Wir suchen also Lösungen der Ungleichung

denn bei ≥ 0 wäre unsere Existenz als Spielbudenbesitzer offensichtlich gefährdet.

Formt man um, dann sieht es einfacher aus. Gesucht sind Lösungen der Ungleichung n + 10•m < 25 .

Es gibt bei einer Ungleichung mit zwei Unbekannten natürlich prinzipiell unendlich viele Lösungen. Das schauen wir uns gleich näher an.

Folie 20

Sie sehen hier Beispiele.

Für n = 2 und m = 1 ist  2 + 10•1 = 12 < 25

Für n = 2 und m = 1,5 ist  2 + 10•1,5 = 17 < 25

Für n = 4 und m = 2 ist  4 + 10•2 = 24 < 25

Diese Gewinne kommen also für Ihre Spielbank in Frage. Ob sich Ihre Kunden aber mit einem allzu kleinen Gewinn wie dem in der ersten oder zweiten Zeile zufriedengeben würden, darf angezweifelt werden.

Folie 21

Sie merken schon. Es ist gar nicht so einfach, hier das rechte Gleichgewicht zu halten. Der Erwartungswert erlaubt allerdings eine gute Beurteilung der Situation.

Folie 22

Das war es für heute. Alles Gute für Sie und schön, dass Sie dabei waren. Bis zum nächsten Mal.