28 Ist Anna etwas zu klein für ihr Alter? Die Normalverteilung.

 

Folie 0

Einen wunderschönen Tag Ihnen allen. Herzlich willkommen zu dieser neuen Folge, in der wir – wie immer – über Mathematik reden. Es geht auch dieses Mal um eine Wahrscheinlichkeitsverteilung. Es ist die sogenannte Normalverteilung, eine wichtige Verteilung mit vielen interessanten Anwendungen.

Folie 1

Wir gehen allgemein von dieser Fragestellung aus:

Mit welcher Wahrscheinlichkeit nimmt eine Zufallsgröße bestimmte Werte an?

Überlegen wir dazu zunächst, was wir in diesem Kontext schon wissen.

Ein einfaches Beispiel ist – wie so oft – der reguläre, sechsseitige Würfel. Jedes der Ergebnisse 1, 2, 3, 4, 5 und 6 tritt mit der gleichen Wahrscheinlichkeit von p = 1/6 auf. Das kann man als Gleichverteilung ansehen.

Wir haben außerdem in der letzten Folge die Binomialverteilung betrachtet und sie tatsächlich mit einer Formel in den Griff bekommen. Klappt das vielleicht auch mit anderen Wahrscheinlichkeitsverteilungen? Ja, das ist durchaus möglich. Und um ein Beispiel dafür geht es heute.

Folie 2

Es gibt natürlich viele (benannte und unbenannte) Wahrscheinlichkeitsverteilungen, die wir sicherlich weder betrachten noch formelmäßig beschreiben können. Wir schauen uns im Folgenden daher nur ein weiteres, aber sehr wichtiges Beispiel an. Es ist die Normalverteilung und sie betrifft – genau wie die Binomialverteilung – eine ganze Klasse von Zufallsexperimenten.

Und darum geht es exemplarisch und in einfachen Worten: Ist Anna etwas zu klein für ihr Alter?

Folie 3

Betrachten wir die Normalverteilung zunächst qualitativ. Sie ist präsent in vielen ganz alltäglichen Zusammenhängen. So sind etwa

• Größe
• Gewicht
• Kopfumfang

bei neugeborenen Babys normalverteilt. Und was heißt das? Qualitativ gesehen ist es einfach: Es gibt einen mittleren Wert und rund um diesen mittleren Wert finden sich die gemessenen Werte relativ nahe mit größerer Wahrscheinlichkeit als weiter von diesem mittleren Wert entfernt.

Folie 4

Betrachten wir die Körpergröße von Kindern. Die WHO, die World Health Organization oder Weltgesundheitsorganisation, hat dazu und zu verschiedenen anderen Merkmalen im Jahr 2006 Daten veröffentlicht. Sie wurden in sechs Staaten erhoben. Das waren Brasilien, Ghana, Indien, Norwegen, Oman und die USA.

In der entsprechenden Publikation finden sich beispielsweise auf Seite 64 in Tabelle 27 Angaben zur Körpergröße neugeborener Mädchen. Schauen wir uns diese Tabelle genauer an.

Folie 5

Das ist ein Ausschnitt aus der Tabelle:

Der mittlere Wert der Größe von Mädchen bei der Geburt ist 49,1 cm groß, die Standardabweichung beträgt SD = 1,9 cm. Auch die Perzentile sind hier aufgeführt. Sie erinnern sich, was Perzentile sind? Es sind die Zahlen in der oberen Zeile der Tabelle und sie geben Prozentsätze an. So bedeutet etwa „75“, dass 75% der neugeborenen Mädchen höchstens so groß sind wie der entsprechende Wert von 50,4 cm.

Wir werden es auf der nächsten Folie noch einmal genauer fassen.

Es sei betont, dass der mittlere Wert hier der Median ist. Er bezeichnet – und das haben wir schon häufiger genutzt– die Marke von 50%.

Folie 6

Worum geht es also bei den Perzentilen?

Nehmen wir an, die gerade geborene Anna misst 46 cm. Dann wäre sie bezüglich der Körpergröße bei den unteren 5% der weiblichen Babys einzuordnen.

Werden 48 cm gemessen, dann würde sie bezüglich der Körpergröße zu den unteren 25% der weiblichen Babys gehören. Allerdings wäre dieser Wert noch innerhalb einer Standardabweichung, die ja mit 1,9 cm angegeben war.

Nehmen wir an, Anna misst 49 cm. Dann läge sie bezüglich der Körpergröße etwa im Mittel der weiblichen Babys und etwa die Hälfte wäre größer bzw. kleiner als sie.

Und 54 cm? Das wäre ganz schön groß, denn 99% der weiblichen Babys kommen kleiner als eine solche Anna auf die Welt.

Folie 7

Aus diesen Werten lassen sich nun die Abweichungen von der mittleren Körpergröße bestimmen. Die Symmetrie dabei ist ziemlich auffällig.

Folie 8

Und das tragen wir in ein Diagramm ein. Die roten Balken zeigen die absoluten Werte in den Perzentilen. Die blauen Balken sollen hingegen die Abweichung vom Median und damit dem Erwartungswert verdeutlichen. Abweichungen nach oben und unten sind in gleicher Weise abgetragen.

Und um diese Abweichung geht es. Es ist sicherlich nicht überraschend, dass sie eine gewisse Symmetrie zeigen und die Abweichungen nach oben und unten ganz ähnlich bei etwa gleichem Abstand zum Median sind.

Man sieht – ggf. mit etwas Phantasie – die Gauß‘sche Glockenkurve.

Folie 9

Betrachten wir noch einmal die Messwerte.

Die Standardabweichung wird von der OECD auf vier Kommastellen genau mit 1,8627 cm angegeben.

Berücksichtigt man eine Standardabweichung (oder mehr), dann kommt man in den Bereich bis 47,3 cm bzw. ab 51,0 cm Körpergröße.

Berücksichtigt man zwei Standardabweichungen (oder mehr), dann kommt man in den Bereich bis 45,4 cm bzw. ab 52,9 cm Körpergröße.

Eine Standardabweichung oder mehr misst man entsprechend bei weniger als den oberen bzw. unteren 25% der neugeborenen Mädchen. Zwei Standardabweichungen sind sehr viel und in diesen Bereich fallen auch weniger als die oberen bzw. unteren 3% der neugeborenen Mädchen.

Folie 10

Und das charakterisiert die Normalverteilung.

Bei einer Normalverteilung liegen 68,3% der Daten in einem Bereich, der durch den

Erwartungswert +/- 1 Standardabweichung bestimmt ist.

Im Beispiel haben also 68,3% der Neugeborenen eine Körpergröße zwischen 47,3 cm und 51,0 cm.

Bei einer Normalverteilung liegen etwa 95,5% der Daten in einem Bereich, der durch den Erwartungswert +/- 2 Standardabweichungen bestimmt ist.

Im Beispiel haben also etwa 95,5% der Neugeborenen eine Körpergröße zwischen 45,4 cm und 52,9 cm.

Folie 11

Aber natürlich wollen wir den Sachverhalt auch noch systematischer betrachten.

Wenn man das macht, dann kommt man von der Binomialverteilung zur Normalverteilung. Für große Stichproben lassen sich nämlich die Histogramme binomialverteilter Zufallsgrößen durch Glockenkurven annähern. Sie erinnern sich? Das hatten wir in der letzten Folge beim 50-maligen Wurf eines Würfels mit den Ergebnissen „6“ oder „keine 6“ in einem Histogramm gesehen.

Es klappt wirklich am besten über entsprechende Simulationen. Glockenkurven können durch den Term

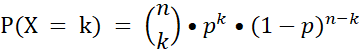
beschrieben werden. Dabei bezeichnet μ den Erwartungswert und σ die Standardabweichung.

Folie 12

Wir definieren.

Lässt sich eine Zufallsgröße mit Erwartungswert μ und Standardabweichung σ durch die Funktion

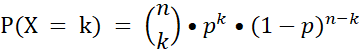
beschreiben, dann heißt sie normalverteilt. Diese Funktion nennt man Wahrscheinlichkeitsdichte.

Eine Zufallsgröße heißt standardnormalverteilt, falls der Erwartungswert μ = 0 und die Standardabweichung σ = 1 ist. Was man dann bekommt, das ist die Gauß‘sche Glockenkurve.

Folie 13

Viele Dinge in unserem Alltag sind normalverteilt oder annähernd normalverteilt. So kann man – und das natürlich bei einer großen Strichprobe – eine Normalverteilung in den diesen Fällen annehmen:

Die Größe und das Gewicht auch von erwachsenen Personen; die Leistungen von Schülerinnen und Schülern im Hochsprung oder Weitsprung; das Gewicht von Eiskugeln, Teepäckchen, Brötchen und Brotlaiben; die Anzahl der Gummibärchen in einer 100 g Tüte.

In allen diesen Fällen gibt es einen mittleren Wert, unter bzw. über dem 50% der Messwerte liegen und um den herum in eher kleinem Abstand dann auch noch die meisten Messwerte liegen werden. Und es wird Abweichungen sowohl nach oben als auch nach unten geben.

Folie 14

Danke, dass Sie heute dabei waren. Wir treffen uns wieder in der nächsten Folge und reden auch dann über Mathematik.