25 Der härteste Brocken der Kombinatorik: Eine völlig ungerechte Verteilung von Äpfeln an Kinder.

 

Folie 0

Herzlich willkommen zu einer neuen Folge. Wir reden heute noch einmal über Kombinatorik und lösen ein Problem, das wir nicht ganz zu Unrecht aufgeschoben haben. Wir verteilen Äpfel an Kinder und lassen dabei jede Gerechtigkeit aus dem Spiel.

Folie 1

Sie erinnern sich an die Urnenmodelle?

Wir haben uns in bereits den ersten Folgen damit beschäftigt und Kugeln aus einer Urne gezogen. Wichtig war die Unterscheidung des Ziehens

• mit und ohne Zurücklegen der Kugel sowie
• mit und ohne Beachtung der Reihenfolge

Kombiniert man diese Möglichkeiten des Ziehens, dann gibt es vier verschiedene Arten es zu tun. Allerdings haben wir bisher nur drei Fälle behandelt.

Lassen Sie uns kurz zurückblicken, welche es waren und lassen Sie uns zumindest die entsprechenden Formeln wiederholen.

Folie 2

Das war der erste Fall, den wir uns angesehen haben: Das Ziehen mit Zurücklegen und mit Beachtung der Reihenfolge. Und das war ein relativ einfacher Fall.

Schauen wir uns das Beispiel an. In dieser Dose sind acht Kugeln in unterschiedlichen Farben. Es gibt also acht Möglichkeiten, eine dieser Kugeln zu ziehen. Macht man das mehrfach hintereinander und legt die Kugel jeweils wieder zurück, dann hat man bei jedem neuen Zug auch diese acht Möglichkeiten. Man kommt beim fünfmaligen Ziehen entsprechend auf

8 • 8 • 8 • 8 • 8 = 8⁵ = 32.768

Möglichkeiten. Das ist das Ziehen mit Zurücklegen und mit Beachtung der Reihenfolge.

Folie 3

Allgemein sieht es so aus: Aus einer Menge mit n Elementen lassen sich

n • n • n • … • n = n^k

sogenannte k-Tupel bilden. Wir hatten das auch Wörter der Länge k genannt.

Folie 4

In einem weiteren Fall ging es darum, ohne Zurücklegen zu ziehen, aber weiterhin die Reihenfolge zu beachten.

Sie sehen das Beispiel. Aus der Dose mit den acht verschiedenen Kugeln kann man zunächst unter acht Kugeln wählen. Im nächsten Schritt fehlt die gezogene Kugel natürlich, sodass man nur noch sieben zur Auswahl hat. Zieht man fünfmal hintereinander, dann ergeben sich 8 • 7 • 6 • 5 • 4 Möglichkeiten. Und das kann man auch als  schreiben.

Folie 5

So sieht es allgemein aus:

Aus einer Menge mit n Elementen kann man  Anordnungen aus k Elementen ziehen. Diese Anordnungen nennt man k-Permutationen.

Folie 6

Und das war der dritte Fall, den wir betrachtet haben. Wir ziehen wieder ohne Zurücklegen und interessieren uns nicht für die Reihenfolge.

Dieses Beispiel kennen Sie schon: Lene verreist gerne, sie hat fünf Kleider. Wie viele Möglichkeiten hat sie, davon drei in ihren Koffer zu packen?

Wiederum gibt es für das erste Kleid fünf Möglichkeiten, für das zweite Kleid noch vier Möglichkeiten und für das dritte Kleid schließlich drei Möglichkeiten.

Ist also 5 • 4 • 3 die Lösung?

Folie 7

Nein, natürlich nicht. Es ist ja völlig egal, ob sie erst das rote und dann das grüne oder aber die beiden in umgekehrter Reihenfolge aus dem Schrank holt. Es gilt also, alle gleichen Kombinationen von Kleidern nur einmal zu zählen.

Folie 8

Und das heißt bei drei Kleidern durch 3! zu dividieren. Es gibt in diesem Fall also

(5 • 4 • 3) : (3 • 2 • 1) =  

unterschiedliche Möglichkeiten.

Folie 9

Allgemein sieht es so aus. Beim Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge geht es um die Anzahl der Teilmengen mit k Elementen aus einer Menge mit n Elementen. Diese Zahl ist  .

Folie 10

Ganz offensichtlich fehlt also noch der Fall, dass wir eine Kugel aus einer Urne ziehen, sie wieder zurücklegen, uns aber nicht für die Reihenfolge interessieren.

Das ist ein Beispiel: Wir verteilen 8 Äpfel auf 5 Kinder. Wie viele verschiedene Verteilungen sind möglich? Dabei nehmen wir ganz bewusst herbe Ungerechtigkeiten in Kauf. Es kann entsprechend auch vorkommen, dass ein Kind keinen Apfel oder, dass es gleich mehrere Äpfel bekommt.

Nehmen Sie sich einen Moment Zeit und überlegen Sie sich, warum dieses Beispiel passt. Wer oder was wird hier eigentlich gezogen?

Folie 11

Nein. Wir stecken natürlich keine Kinder in eine Urne.

Aber wie wäre es mit fünf Kugeln, die wir mit den Zahlen von 1 bis 5 beschriften. Jede Zahl steht für ein Kind. Wird eine Kugel gezogen, dann bekommt das entsprechende Kind einen Apfel.

Das ist dann offensichtlich das Ziehen mit Zurücklegen ohne Beachtung der Reihenfolge.

Das Problem ist nun, ein passendes Modell für diese Situation zu finden, um daraus dann die Anzahl der Möglichkeiten (und eine sinnvolle Formel) abzuleiten.

Folie 12

Lassen Sie uns eine Tabelle nutzen. Hier sind exemplarisch drei mögliche Verteilungen eingetragen. Im ersten Fall geht Kind 3 leer aus, im zweiten Fall ist es Kind 5 und Kind 4 bekommt recht viele. Im dritten Fall schließlich geht Kind 5 mit allen acht Äpfeln nach Hause. Wie gesagt, wir interessieren uns hier überhaupt nicht für Gerechtigkeit.

Und ganz klar, es gibt viele andere Möglichkeiten für eine solche Verteilung.

Folie 13

Und nun bitte ich Sie, die Situation etwas anders zu sehen. Vergessen Sie die Kinder, vergessen Sie die Äpfel, nehmen Sie die Tabelle als ein abstraktes Etwas.

Jede Tabellenzeile lässt sich doch als eine Folge von 5 + 8 - 1 Zeichen auffassen. Es gibt 8 Kreuze und 4 Striche. Es sind die Striche, die die einzelnen Felder einer Zeile voneinander trennen. Und das sind natürlich fünf Felder – genau so, wie die Aufgabenstellung sie benennt. Wir schreiben daher nicht 4 Striche, sondern wählen die Bezeichnung 5-1.

Folie 14

Noch einmal, jede Tabellenzeile lässt sich als eine Folge von 5 + 8 - 1 Zeichen, nämlich 8 Kreuzen und 4 = 5 - 1 Strichen auffassen. Wir suchen also die möglichen Plätze für 8 Kreuze.

Genau das hatten wir aber gerade.

Für die Verteilung der 8 Kreuze auf die 5 + 8 -1 Zeichenstellen gibt es, wenn die Reihenfolge egal ist und keine Wiederholungen gestattet sind, genau

Möglichkeiten.

Folie 15

Das kann man leicht berechnen und man bekommt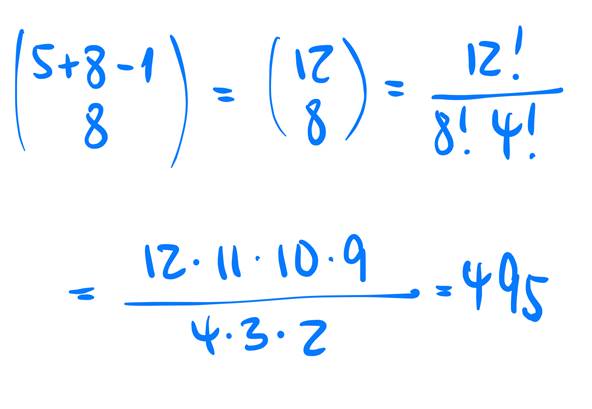

Folie 16

Ganz allgemein sieht es so aus: Wenn wir aus einer Urne mit n Objekten mit Zurücklegen und ohne Beachtung der Reihenfolge k Objekte auswählen, dann gibt es dafür

Möglichkeiten.

Folie 17

Ich weiß nicht, wie gut Ihnen das Modell gefallen hat. Haben Sie Lust auf einen zweiten Erklärungsansatz? Hier ist ein weiterer Zugang zur Lösung des Problems.

Wieder gehen wir von 8 Äpfeln A₁, A₂, … , A₈ und 5 Kindern K₁, … , K₅ aus. Wir tragen beide als Punkte in ein Diagramm ein.

Folie 18

Man kann oberhalb der Kinder die Äpfel einzeichnen, die sie jeweils bekommen. Im Beispiel hier bekommen das erste und das dritte Kind je zwei Äpfel, das vierte einen Apfel und das fünfte drei Äpfel. Das zweite Kind geht leer aus. Wenn man Kinder und Äpfel, also x-Achse und die y-Achse beachtet, dann ist jede mögliche Zuordnung ein Weg in diesem Diagramm.

Folie 19

Das ist ein anderer Weg, aber er ist genauso lang. Eigentlich ganz einfach. Es gibt 8 senkrechte Verbindungen, die jeweils für einen Apfel stehen und vier waagrechte Verbindungen, die Zwischenräume zwischen den Kindern auf der x-Achse

Folie 20

Hier ist noch ein solcher möglicher Weg. Und wie sieht es aus, wenn man systematisch vorgeht?

Dann suchen wir alle Wege der Länge 12, die aus 8 senkrechten und 4 waagrechten Teilstücken bestehen.

Und offensichtlich ist es so: Man wählt die senkrechten Teilstücke aus, die waagrechten sind dann fix.

Damit sind wir wieder bei der Grundidee, dass „8 aus 12“ gewählt werden.

Folie 21

Beim Ziehen mit Zurücklegen und ohne Beachtung der Reihenfolge sieht es so aus, dass wir allgemein die Anzahl der k-Kombinationen mit Wiederholungen aus einer Menge mit n Elementen bestimmen. Und das ist

 

Eine k-Kombination mit Wiederholung ist noch einmal ein anderer Ausdruck für ein k-Tupel oder ein Wort der Länge k.

Folie 22

Eigentlich müsste man bei den Wegen der Länge 12 auch zuerst die waagrechten Teilstücke wählen können, oder? Dann wären eben die senkrechten Teilstücke fix.

Kann das klappen? Gibt das nicht eine ganz andere Zahl?

Nein, das geht ohne Probleme.  Wir wissen ja:

Folie 23

Mögen Sie selbst einmal ein Beispiel rechnen? Hier ist es.

Sebastian hat 6 identische Smiley-Sticker. Er möchte damit 10 Päckchen bekleben. Wie viele (ggf. auch völlig ungerechte) Möglichkeiten hat er, seine Sticker auf die Päckchen zu verteilen? Machen Sie eine kurze Pause, überlegen und rechnen Sie.

Folie 24

Sebastian hat 6 identische Smiley-Sticker, also ist n = 6. Er möchte damit 10 Päckchen bekleben, also ist k = 10. Und damit rechnet man:

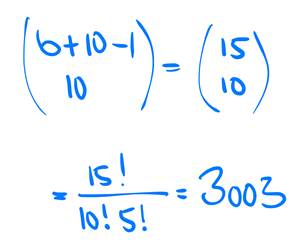
Folie 25

Lassen Sie uns zusammenfassen.

Für die Auswahl von k Elementen aus einer Menge mit n Elementen gibt es vier Möglichkeiten. Man kann mit oder ohne Zurücklegen ziehen, man kann die Reihenfolge beachten oder nicht. Für jeden dieser vier Fälle haben wir eine Formel erarbeitet und die sehen Sie hier in der Tafel.

Aber vergessen Sie bitte nicht, dass es gerade im Unterricht nicht darum gehen kann, eine Formel anzuwenden. Man sollte sie wirklich vorher verstanden haben und das heißt, man sollte sie sich auch erarbeitet haben.

Folie 26

Danke, dass Sie dabei waren. Ich freue mich darauf, Sie in der nächsten Folge zu sehen, in der wir wieder über Mathematik reden.